


Next: 8.5 Off-Policy Bootstrapping
Up: 8 Generalization and Function
Previous: 8.3.4 Kanerva Coding
We now extend value-prediction methods using function approximation to
control methods, following the pattern of GPI. First we extend the the
state-value prediction methods to action-value prediction methods, then we
combine them with policy-improvement and action-selection techniques. As
usual, the problem of ensuring exploration is solved by pursuing either an
on-policy or an off-policy approach.
The extension to action-value prediction is straightforward. In this case it is
the action-value function, 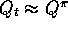 , that is represented as a
parameterized functional form with parameter vector
, that is represented as a
parameterized functional form with parameter vector  . Whereas before we
considered training examples of the form
. Whereas before we
considered training examples of the form 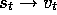 , now we consider
examples of the form
, now we consider
examples of the form 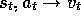 . The example output,
. The example output,
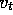 , can be any approximation of
, can be any approximation of 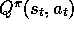 , including the usual
backed-up values such as the full Monte-Carlo return,
, including the usual
backed-up values such as the full Monte-Carlo return,
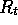 , or the 1-step Sarsa-style return,
, or the 1-step Sarsa-style return, 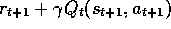 .
The general gradient-descent update for action-value prediction is
.
The general gradient-descent update for action-value prediction is
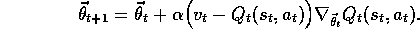
For example, the backward view of the action-value method analogous
to TD(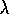 )
is
)
is

where

and
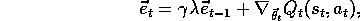
with 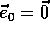 . We call this method gradient-descent
Sarsa(
. We call this method gradient-descent
Sarsa(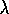 )
, particularly when it is elaborated to form a full control method. For
a constant policy, this method converges in the same way that TD(
)
, particularly when it is elaborated to form a full control method. For
a constant policy, this method converges in the same way that TD(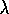 )
does,
with the same kind of error bound (8.9).
)
does,
with the same kind of error bound (8.9).
To form control methods, we need to couple such action-value prediction methods
with techniques for policy improvement and action selection. Suitable
techniques applicable to continuous actions, or to actions from large discrete
sets, are a topic of ongoing research with as yet no clear resolution. On the
other hand, if the action set is discrete and not too large, then we can
use the techniques already developed in previous chapters. That is, for each
possible action, a, available in the current state, 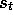 , we can compute
, we can compute
 and then find the greedy action
and then find the greedy action 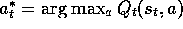 .
Policy improvement is done by changing the estimation policy to the greedy
policy (in off-policy methods) or to a soft approximation of the greedy
policy such as the
.
Policy improvement is done by changing the estimation policy to the greedy
policy (in off-policy methods) or to a soft approximation of the greedy
policy such as the
 -greedy policy (in on-policy methods). Actions are selected according to this
same policy in on-policy methods, or by an arbitrary policy in off-policy methods.
-greedy policy (in on-policy methods). Actions are selected according to this
same policy in on-policy methods, or by an arbitrary policy in off-policy methods.
Initialize 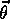 arbitrarily and
arbitrarily and 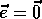 Repeat (for each episode):
Repeat (for each episode):
 For all
For all 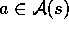 :
:

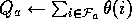
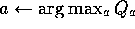 With probability
With probability  :
: 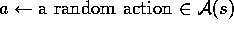 Repeat (for each step of episode):
Repeat (for each step of episode):
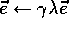 For all
For all 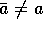 : (optional block for replacing traces)
For all
: (optional block for replacing traces)
For all 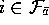 :
:
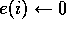 For all
For all 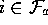 :
:
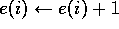 (accumulating traces)
or
(accumulating traces)
or 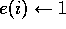 (replacing traces)
Take action a, observe reward, r, and next state,
(replacing traces)
Take action a, observe reward, r, and next state, 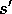
 For all
For all 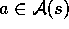 :
:

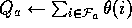
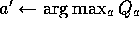 With probability
With probability  :
: 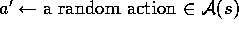
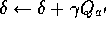
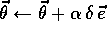
 until
until 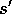 is terminal
is terminal
Figure 8.8: Linear, gradient-descent Sarsa(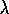 )
with binary features and
)
with binary features and  -greedy
policy. Updates for both accumulating and replacing traces are specified,
including the option (when using replacing traces) of clearing the traces
of non-selected actions.
-greedy
policy. Updates for both accumulating and replacing traces are specified,
including the option (when using replacing traces) of clearing the traces
of non-selected actions.
Initialize 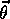 arbitrarily and
arbitrarily and 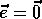 Repeat (for each episode):
Repeat (for each episode):
 For all
For all  :
:

 Repeat (for each step of episode):
With probability
Repeat (for each step of episode):
With probability 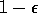 :
:
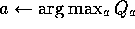
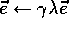 else
else

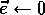 For all
For all 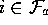 :
: 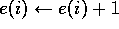 Take action a, observe reward, r, and next state,
Take action a, observe reward, r, and next state, 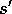
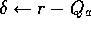 For all
For all 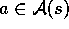 :
:

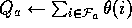
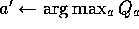
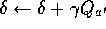
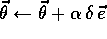 until
until 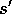 is terminal
is terminal
Figure 8.9: A linear, gradient-descent version of Watkins's Q(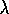 )
with binary
features,
)
with binary
features,  -greedy policy, and accumulating traces.
-greedy policy, and accumulating traces.
Figures 8.8 and 8.9 show examples of on-policy (Sarsa(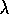 )
)
and off-policy (Watkins's Q(
)
)
and off-policy (Watkins's Q(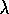 )
) control methods using function approximation.
Both methods use linear, gradient-descent function approximation with binary
features, such as in tile coding and Kanerva coding. Both methods use an
)
) control methods using function approximation.
Both methods use linear, gradient-descent function approximation with binary
features, such as in tile coding and Kanerva coding. Both methods use an
 -greedy policy for action selection, and the Sarsa method uses it for GPI as
well. Both compute the sets of present features,
-greedy policy for action selection, and the Sarsa method uses it for GPI as
well. Both compute the sets of present features, 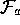 , corresponding to the
current state and all possible actions, a. If the value function for each
action is a separate linear function of the same features (a common case), then
the indices of all the
, corresponding to the
current state and all possible actions, a. If the value function for each
action is a separate linear function of the same features (a common case), then
the indices of all the 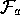 may be the same except for an offset, simplifying
the computation significantly.
may be the same except for an offset, simplifying
the computation significantly.
All the methods we have discussed above have used accumulating
eligibility traces. Although replacing traces (Section 7.8) are known to have
advantages in tabular methods, they do not directly extend to the use of function
approximation. Recall that the idea of replacing traces is to reset a state's
trace to 1 each time it is visited instead of incrementing it by 1.
But with function approximation there is no single trace corresponding to
a state, just a trace for each component of 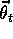 , each of which corresponds
to many states. One approach that seems to work well for linear,
gradient-descent function approximation with binary features is to treat the
features as if they were states for the purposes of replacing traces. That is,
each time a state is encountered that has feature i, the trace for
feature i is set to 1 rather than being incremented by 1 as it would be with
accumulating traces.
, each of which corresponds
to many states. One approach that seems to work well for linear,
gradient-descent function approximation with binary features is to treat the
features as if they were states for the purposes of replacing traces. That is,
each time a state is encountered that has feature i, the trace for
feature i is set to 1 rather than being incremented by 1 as it would be with
accumulating traces.
When working with state-action traces, it may also be useful to clear (set
to zero) the traces of all non-selected actions in the states encountered (see
Section 7.8). This idea can also be extended to the case of linear function
approximation with binary features. For each state encountered, we first clear
the traces of all features for the state and the actions not selected, then
we set to
1 the traces of the features for the state and the action that was selected.
As we noted for the tabular case, this may or may not be the best way to
proceed when using replacing traces. A procedural specification of both
kinds of traces, including the optional clearing for non-selected actions,
is given for the Sarsa algorithm in Figure 8.8.
Example  .
. The Mountain-Car Task.
Consider the task of driving an underpowered car up a steep mountain road, as
suggested by the diagram in the upper left of Figure 8.10. The
difficulty is that gravity is stronger than the car's engine, and even at full
throttle it cannot accelerate up the steep slope. The only solution is to
first move away from the goal and up the opposite slope on the left. Then,
by applying full throttle the car can build up enough inertia to carry
it up the steep slope even though it is slowing down the whole way. This is a
simple example of a continuous control task where things have to get worse in a
sense (farther from the goal) before they can get
better. Many control methodologies have great difficulties with tasks of
this kind unless explicitly aided by a human designer.
The Mountain-Car Task.
Consider the task of driving an underpowered car up a steep mountain road, as
suggested by the diagram in the upper left of Figure 8.10. The
difficulty is that gravity is stronger than the car's engine, and even at full
throttle it cannot accelerate up the steep slope. The only solution is to
first move away from the goal and up the opposite slope on the left. Then,
by applying full throttle the car can build up enough inertia to carry
it up the steep slope even though it is slowing down the whole way. This is a
simple example of a continuous control task where things have to get worse in a
sense (farther from the goal) before they can get
better. Many control methodologies have great difficulties with tasks of
this kind unless explicitly aided by a human designer.

Figure 8.10: The mountain-car task (upper left panel) and the cost-to-go function
(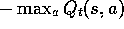 ) learned during one run.
) learned during one run.
The reward in this problem is -1 on all time steps until the car has moved
past its goal position at the top of the mountain, which ends the episode.
There are three possible actions: full throttle forward (+1), full
throttle reverse (-1), and zero throttle (0). The car moves according to
a simplified physics. It's position,
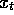 , and velocity,
, and velocity, 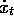 , are given by
, are given by

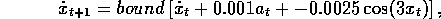
where the bound operation enforces 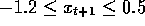 and
and  . When
. When 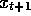 reached the left bound, then
reached the left bound, then 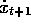 was reset to zero. When it reached right bound, then the goal was reached
and the episode was terminated. Each episode started from a random position and
velocity uniformly chosen from these ranges. To convert the two continuous state
variables to binary features, we used grid-tilings exactly as in
Figure 8.5. We used ten
was reset to zero. When it reached right bound, then the goal was reached
and the episode was terminated. Each episode started from a random position and
velocity uniformly chosen from these ranges. To convert the two continuous state
variables to binary features, we used grid-tilings exactly as in
Figure 8.5. We used ten 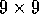 tilings, each offset by a random
fraction of a tile width.
tilings, each offset by a random
fraction of a tile width.
The Sarsa algorithm in Figure 8.8 (using replace
traces and the optional clearing) readily solved this task, learning
a near optimal policy within 100 episodes. Figure 8.10
shows the negative of the value function (the cost-to-go function)
learned on one run, using the parameters
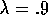 ,
, 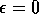 , and
, and  (
(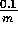 ). The initial action values were
all zero, which was optimistic (all true values are negative in this task),
causing extensive exploration to occur even though the exploration parameter,
). The initial action values were
all zero, which was optimistic (all true values are negative in this task),
causing extensive exploration to occur even though the exploration parameter,  ,
was 0. This can be seen in the middle-top panel of the figure, labeled ``Step
428." At this time not even one episode has been completed, but the car has
oscillated back and forth in the valley, following circular trajectories in state
space. All the states visited frequently are valued worse than
unexplored states, because the actual rewards have been worse than what was
(unrealistically) expected. This continually drives the agent away from wherever
it has been to explore new states, until a solution is found.
Figure 8.11 shows the results of a detailed study of the effect
of the parameters
,
was 0. This can be seen in the middle-top panel of the figure, labeled ``Step
428." At this time not even one episode has been completed, but the car has
oscillated back and forth in the valley, following circular trajectories in state
space. All the states visited frequently are valued worse than
unexplored states, because the actual rewards have been worse than what was
(unrealistically) expected. This continually drives the agent away from wherever
it has been to explore new states, until a solution is found.
Figure 8.11 shows the results of a detailed study of the effect
of the parameters 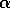 and
and 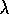 , and of the kind of traces, on the rate of learning
on this task.
, and of the kind of traces, on the rate of learning
on this task.
Figure 8.11: The effect of 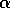 ,
,  , and the kind of traces on early performance on the
Mountain-Car task. This study used five
, and the kind of traces on early performance on the
Mountain-Car task. This study used five 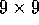 tilings.
tilings.
Exercise 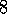 .
. *
*
Describe how the actor-critic control method could be combined with
gradient-descent function approximation.



Next: 8.5 Off-Policy Bootstrapping
Up: 8 Generalization and Function
Previous: 8.3.4 Kanerva Coding
Richard Sutton
Sat May 31 15:08:20 EDT 1997
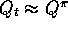 , that is represented as a
parameterized functional form with parameter vector
, that is represented as a
parameterized functional form with parameter vector  . Whereas before we
considered training examples of the form
. Whereas before we
considered training examples of the form 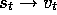 , now we consider
examples of the form
, now we consider
examples of the form 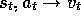 . The example output,
. The example output,
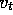 , can be any approximation of
, can be any approximation of 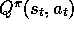 , including the usual
backed-up values such as the full Monte-Carlo return,
, including the usual
backed-up values such as the full Monte-Carlo return,
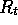 , or the 1-step Sarsa-style return,
, or the 1-step Sarsa-style return, 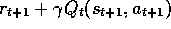 .
The general gradient-descent update for action-value prediction is
.
The general gradient-descent update for action-value prediction is



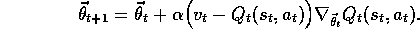
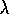 )
is
)
is


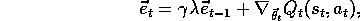
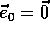 . We call this method gradient-descent
Sarsa(
. We call this method gradient-descent
Sarsa(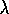 )
, particularly when it is elaborated to form a full control method. For
a constant policy, this method converges in the same way that TD(
)
, particularly when it is elaborated to form a full control method. For
a constant policy, this method converges in the same way that TD( )
does,
with the same kind of error bound (
)
does,
with the same kind of error bound (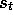 , we can compute
, we can compute
 and then find the greedy action
and then find the greedy action 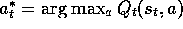 .
Policy improvement is done by changing the estimation policy to the greedy
policy (in off-policy methods) or to a soft approximation of the greedy
policy such as the
.
Policy improvement is done by changing the estimation policy to the greedy
policy (in off-policy methods) or to a soft approximation of the greedy
policy such as the
 -greedy policy (in on-policy methods). Actions are selected according to this
same policy in on-policy methods, or by an arbitrary policy in off-policy methods.
-greedy policy (in on-policy methods). Actions are selected according to this
same policy in on-policy methods, or by an arbitrary policy in off-policy methods.
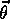 arbitrarily and
arbitrarily and 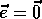 Repeat (for each episode):
Repeat (for each episode):
 For all
For all 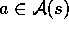 :
:

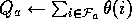
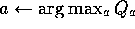 With probability
With probability  :
: 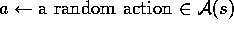 Repeat (for each step of episode):
Repeat (for each step of episode):
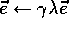 For all
For all 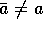 : (optional block for replacing traces)
For all
: (optional block for replacing traces)
For all 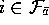 :
:
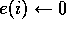 For all
For all 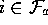 :
:
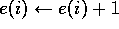 (accumulating traces)
or
(accumulating traces)
or 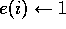 (replacing traces)
Take action a, observe reward, r, and next state,
(replacing traces)
Take action a, observe reward, r, and next state, 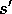
 For all
For all 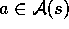 :
:

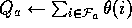
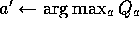 With probability
With probability  :
: 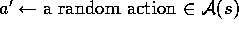
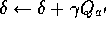
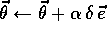
 until
until 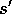 is terminal
is terminal
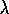 )
with binary features and
)
with binary features and  -greedy
policy. Updates for both accumulating and replacing traces are specified,
including the option (when using replacing traces) of clearing the traces
of non-selected actions.
-greedy
policy. Updates for both accumulating and replacing traces are specified,
including the option (when using replacing traces) of clearing the traces
of non-selected actions.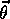 arbitrarily and
arbitrarily and 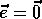 Repeat (for each episode):
Repeat (for each episode):
 For all
For all  :
:

 Repeat (for each step of episode):
With probability
Repeat (for each step of episode):
With probability 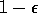 :
:
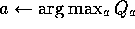
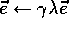 else
else

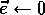 For all
For all 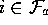 :
: 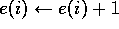 Take action a, observe reward, r, and next state,
Take action a, observe reward, r, and next state, 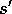
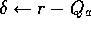 For all
For all 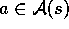 :
:

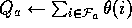
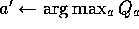
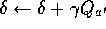
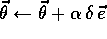 until
until 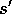 is terminal
is terminal
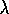 )
with binary
features,
)
with binary
features,  -greedy policy, and accumulating traces.
-greedy policy, and accumulating traces.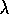 )
)
and off-policy (Watkins's Q(
)
)
and off-policy (Watkins's Q(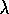 )
) control methods using function approximation.
Both methods use linear, gradient-descent function approximation with binary
features, such as in tile coding and Kanerva coding. Both methods use an
)
) control methods using function approximation.
Both methods use linear, gradient-descent function approximation with binary
features, such as in tile coding and Kanerva coding. Both methods use an
 -greedy policy for action selection, and the Sarsa method uses it for GPI as
well. Both compute the sets of present features,
-greedy policy for action selection, and the Sarsa method uses it for GPI as
well. Both compute the sets of present features, 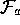 , corresponding to the
current state and all possible actions, a. If the value function for each
action is a separate linear function of the same features (a common case), then
the indices of all the
, corresponding to the
current state and all possible actions, a. If the value function for each
action is a separate linear function of the same features (a common case), then
the indices of all the 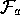 may be the same except for an offset, simplifying
the computation significantly.
may be the same except for an offset, simplifying
the computation significantly.
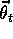 , each of which corresponds
to many states. One approach that seems to work well for linear,
gradient-descent function approximation with binary features is to treat the
features as if they were states for the purposes of replacing traces. That is,
each time a state is encountered that has feature i, the trace for
feature i is set to 1 rather than being incremented by 1 as it would be with
accumulating traces.
, each of which corresponds
to many states. One approach that seems to work well for linear,
gradient-descent function approximation with binary features is to treat the
features as if they were states for the purposes of replacing traces. That is,
each time a state is encountered that has feature i, the trace for
feature i is set to 1 rather than being incremented by 1 as it would be with
accumulating traces.
 .
. The Mountain-Car Task.
Consider the task of driving an underpowered car up a steep mountain road, as
suggested by the diagram in the upper left of Figure
The Mountain-Car Task.
Consider the task of driving an underpowered car up a steep mountain road, as
suggested by the diagram in the upper left of Figure 
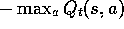 ) learned during one run.
) learned during one run.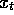 , and velocity,
, and velocity, 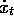 , are given by
, are given by

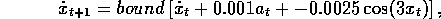
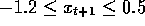 and
and  . When
. When 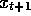 reached the left bound, then
reached the left bound, then 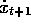 was reset to zero. When it reached right bound, then the goal was reached
and the episode was terminated. Each episode started from a random position and
velocity uniformly chosen from these ranges. To convert the two continuous state
variables to binary features, we used grid-tilings exactly as in
Figure
was reset to zero. When it reached right bound, then the goal was reached
and the episode was terminated. Each episode started from a random position and
velocity uniformly chosen from these ranges. To convert the two continuous state
variables to binary features, we used grid-tilings exactly as in
Figure 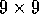 tilings, each offset by a random
fraction of a tile width.
tilings, each offset by a random
fraction of a tile width.
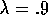 ,
, 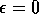 , and
, and  (
(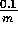 ). The initial action values were
all zero, which was optimistic (all true values are negative in this task),
causing extensive exploration to occur even though the exploration parameter,
). The initial action values were
all zero, which was optimistic (all true values are negative in this task),
causing extensive exploration to occur even though the exploration parameter,  ,
was 0. This can be seen in the middle-top panel of the figure, labeled ``Step
428." At this time not even one episode has been completed, but the car has
oscillated back and forth in the valley, following circular trajectories in state
space. All the states visited frequently are valued worse than
unexplored states, because the actual rewards have been worse than what was
(unrealistically) expected. This continually drives the agent away from wherever
it has been to explore new states, until a solution is found.
Figure
,
was 0. This can be seen in the middle-top panel of the figure, labeled ``Step
428." At this time not even one episode has been completed, but the car has
oscillated back and forth in the valley, following circular trajectories in state
space. All the states visited frequently are valued worse than
unexplored states, because the actual rewards have been worse than what was
(unrealistically) expected. This continually drives the agent away from wherever
it has been to explore new states, until a solution is found.
Figure 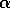 and
and 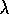 , and of the kind of traces, on the rate of learning
on this task.
, and of the kind of traces, on the rate of learning
on this task.
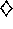

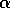 ,
, 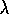 , and the kind of traces on early performance on the
Mountain-Car task. This study used five
, and the kind of traces on early performance on the
Mountain-Car task. This study used five 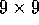 tilings.
tilings. .
.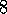 *
*