Next: 7.6 Q()
Up: 7 Eligibility Traces
Previous: 7.4 Equivalence of the
How can eligibility traces be used not just for prediction, as in
TD(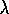 )
, but for control? As usual, the main idea of one popular approach is
simply to learn action values,
)
, but for control? As usual, the main idea of one popular approach is
simply to learn action values, 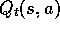 , rather than state values,
, rather than state values, 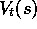 .
In this section we show how eligibility traces can be combined
with Sarsa in a straightforward way to produce an on-policy TD control
method. The eligibility-trace version of Sarsa we call Sarsa (
.
In this section we show how eligibility traces can be combined
with Sarsa in a straightforward way to produce an on-policy TD control
method. The eligibility-trace version of Sarsa we call Sarsa (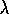 )
, and
the original version presented in the previous chapter we henceforth call
1-step Sarsa.
)
, and
the original version presented in the previous chapter we henceforth call
1-step Sarsa.
The idea in Sarsa(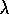 )
is to apply the TD(
)
is to apply the TD(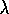 )
prediction method to state-action
pairs rather than to states.
Obviously, then, we need a trace not
just for each state, but for each state-action pair. Let
)
prediction method to state-action
pairs rather than to states.
Obviously, then, we need a trace not
just for each state, but for each state-action pair. Let 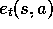 denote the
trace for state-action pair
s,a. Otherwise the method is just like TD(
denote the
trace for state-action pair
s,a. Otherwise the method is just like TD(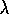 )
, substituting state-action
variables for state variables (
)
, substituting state-action
variables for state variables (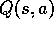 for
for 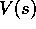 and
and 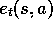 for
for 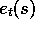 ):
):
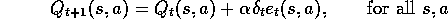
where
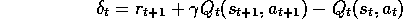
and
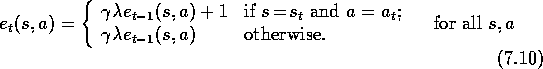
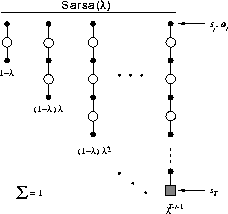
Figure 7.10: Sarsa's backup diagram.
Figure 7.10 shows the backup diagram for Sarsa(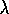 )
. Notice the
similarity to the diagram of the TD(
)
. Notice the
similarity to the diagram of the TD(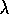 )
algorithm (Figure 7.3).
The first backup looks ahead one full step, to the next state-action pair, the
second looks ahead two steps, etc. A final backup is based on the complete
return. The weighting of each backup is just as in TD(
)
algorithm (Figure 7.3).
The first backup looks ahead one full step, to the next state-action pair, the
second looks ahead two steps, etc. A final backup is based on the complete
return. The weighting of each backup is just as in TD(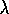 )
and the
)
and the 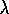 -return
algorithm.
-return
algorithm.
1-step Sarsa and Sarsa( )
are on-policy algorithms, meaning that they approximate
)
are on-policy algorithms, meaning that they approximate
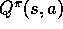 , the action values for the current policy,
, the action values for the current policy,  , then improve the
policy gradually based on the approximate values for the current policy. The
policy improvement can be done in many different ways, as we have seen throughout
this book. For example, the simplest approach is to use the
, then improve the
policy gradually based on the approximate values for the current policy. The
policy improvement can be done in many different ways, as we have seen throughout
this book. For example, the simplest approach is to use the  -greedy
policy with respect to the current action-value estimates.
Figure 7.11 shows the complete Sarsa(
-greedy
policy with respect to the current action-value estimates.
Figure 7.11 shows the complete Sarsa(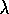 )
algorithm for this
case.
)
algorithm for this
case.
Initialize 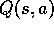 arbitrarily and
arbitrarily and 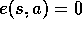 ,
, 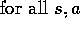 Repeat (for each episode):
Initialize s, a
Repeat (for each step of episode):
Take action a, observe r,
Repeat (for each episode):
Initialize s, a
Repeat (for each step of episode):
Take action a, observe r, 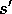 Choose
Choose 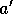 from
from 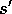 using policy derived from Q
(e.g.,
using policy derived from Q
(e.g.,  -greedy)
-greedy)
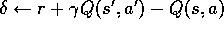
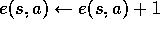 For all s,a:
For all s,a:
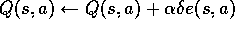
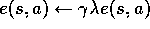
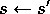 ;
; 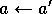 until s is terminal
until s is terminal
Figure 7.11: Tabular Sarsa(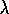 )
.
)
.

Figure 7.12: Gridworld example of the speedup of policy learning due to the use
of eligibility traces. In one episode, 1-step methods strengthen only the last
action leading to an unusually high reward, whereas eligibility trace methods
can strengthen the whole sequence of actions.
Example 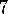 .
. Traces in Gridworld.
The use of eligibility traces can substantially increase the efficiency of
control algorithms. The reason for this is illustrated by the gridworld example
in Figure 7.12. The first panel shows the path taken by
an agent in a single episode, ending at a location of high reward, marked by the
`*'. In this example the values were all initially 0, and all rewards were zero
except for a positive reward at the `*' location. The arrows in the other two
panels show which action values were strengthened as a result of this path by
1-step Sarsa and Sarsa(
Traces in Gridworld.
The use of eligibility traces can substantially increase the efficiency of
control algorithms. The reason for this is illustrated by the gridworld example
in Figure 7.12. The first panel shows the path taken by
an agent in a single episode, ending at a location of high reward, marked by the
`*'. In this example the values were all initially 0, and all rewards were zero
except for a positive reward at the `*' location. The arrows in the other two
panels show which action values were strengthened as a result of this path by
1-step Sarsa and Sarsa(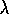 )
methods. The 1-step method strengthens
only the last action of the sequence of actions that led to the high reward,
whereas the trace method strengthens many actions of the sequence. The degree of
strengthening (indicated by the size of the arrows) falls off (according to
)
methods. The 1-step method strengthens
only the last action of the sequence of actions that led to the high reward,
whereas the trace method strengthens many actions of the sequence. The degree of
strengthening (indicated by the size of the arrows) falls off (according to 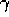
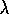 )
with steps from the reward. In this example,
)
with steps from the reward. In this example, 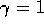 and
and 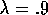 .
.



Next: 7.6 Q()
Up: 7 Eligibility Traces
Previous: 7.4 Equivalence of the
Richard Sutton
Fri May 30 15:01:47 EDT 1997
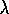 )
, but for control? As usual, the main idea of one popular approach is
simply to learn action values,
)
, but for control? As usual, the main idea of one popular approach is
simply to learn action values, 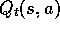 , rather than state values,
, rather than state values, 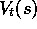 .
In this section we show how eligibility traces can be combined
with Sarsa in a straightforward way to produce an on-policy TD control
method. The eligibility-trace version of Sarsa we call Sarsa (
.
In this section we show how eligibility traces can be combined
with Sarsa in a straightforward way to produce an on-policy TD control
method. The eligibility-trace version of Sarsa we call Sarsa (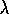 )
, and
the original version presented in the previous chapter we henceforth call
1-step Sarsa.
)
, and
the original version presented in the previous chapter we henceforth call
1-step Sarsa.



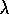 )
is to apply the TD(
)
is to apply the TD(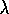 )
prediction method to state-action
pairs rather than to states.
Obviously, then, we need a trace not
just for each state, but for each state-action pair. Let
)
prediction method to state-action
pairs rather than to states.
Obviously, then, we need a trace not
just for each state, but for each state-action pair. Let 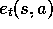 denote the
trace for state-action pair
s,a. Otherwise the method is just like TD(
denote the
trace for state-action pair
s,a. Otherwise the method is just like TD(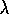 )
, substituting state-action
variables for state variables (
)
, substituting state-action
variables for state variables (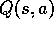 for
for 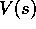 and
and 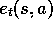 for
for 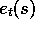 ):
):
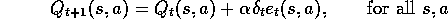
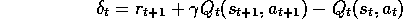
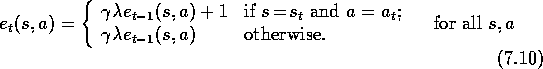

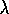 )
. Notice the
similarity to the diagram of the TD(
)
. Notice the
similarity to the diagram of the TD(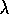 )
algorithm (Figure
)
algorithm (Figure 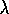 )
and the
)
and the 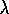 -return
algorithm.
-return
algorithm.
 )
are on-policy algorithms, meaning that they approximate
)
are on-policy algorithms, meaning that they approximate
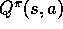 , the action values for the current policy,
, the action values for the current policy,  , then improve the
policy gradually based on the approximate values for the current policy. The
policy improvement can be done in many different ways, as we have seen throughout
this book. For example, the simplest approach is to use the
, then improve the
policy gradually based on the approximate values for the current policy. The
policy improvement can be done in many different ways, as we have seen throughout
this book. For example, the simplest approach is to use the  -greedy
policy with respect to the current action-value estimates.
Figure
-greedy
policy with respect to the current action-value estimates.
Figure 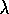 )
algorithm for this
case.
)
algorithm for this
case.
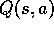 arbitrarily and
arbitrarily and 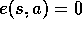 ,
, 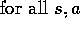 Repeat (for each episode):
Initialize s, a
Repeat (for each step of episode):
Take action a, observe r,
Repeat (for each episode):
Initialize s, a
Repeat (for each step of episode):
Take action a, observe r, 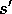 Choose
Choose 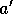 from
from 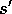 using policy derived from Q
(e.g.,
using policy derived from Q
(e.g.,  -greedy)
-greedy)
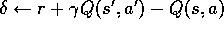
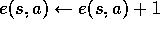 For all s,a:
For all s,a:
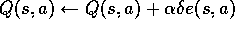
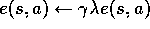
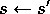 ;
; 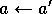 until s is terminal
until s is terminal
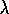 )
.
)
.
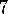 .
.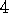 Traces in Gridworld.
The use of eligibility traces can substantially increase the efficiency of
control algorithms. The reason for this is illustrated by the gridworld example
in Figure
Traces in Gridworld.
The use of eligibility traces can substantially increase the efficiency of
control algorithms. The reason for this is illustrated by the gridworld example
in Figure 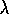 )
methods. The 1-step method strengthens
only the last action of the sequence of actions that led to the high reward,
whereas the trace method strengthens many actions of the sequence. The degree of
strengthening (indicated by the size of the arrows) falls off (according to
)
methods. The 1-step method strengthens
only the last action of the sequence of actions that led to the high reward,
whereas the trace method strengthens many actions of the sequence. The degree of
strengthening (indicated by the size of the arrows) falls off (according to 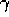
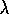 )
with steps from the reward. In this example,
)
with steps from the reward. In this example, 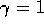 and
and 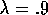 .
.