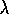 )
and
Peng's Q (
)
and
Peng's Q (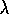 )
after the researchers how first proposed them. First we describe
Watkins's Q(
)
after the researchers how first proposed them. First we describe
Watkins's Q(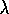 )
.
)
.



Two different methods have been proposed that combine eligibility traces and
Q-learning, which we call Watkins's Q (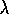 )
and
Peng's Q (
)
and
Peng's Q (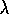 )
after the researchers how first proposed them. First we describe
Watkins's Q(
)
after the researchers how first proposed them. First we describe
Watkins's Q(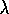 )
.
)
.
Recall that Q-learning is an off-policy method, meaning that the
policy learned about need not be the same as the one used to select actions. In
particular, Q-learning learns about the greedy policy while it typically follows a
policy involving exploratory actions---occasional selections of actions that are
suboptimal according to
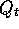 . Because of this, special care is required when introducing eligibility
traces.
. Because of this, special care is required when introducing eligibility
traces.
Suppose we are backing up the state-action pair 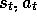 at time t. Suppose that on the successive two time steps the agent
selects the greedy action, but on the third, at time t+3, the agent selects
an exploratory, non-greedy action. In learning about the value of the greedy
policy at
at time t. Suppose that on the successive two time steps the agent
selects the greedy action, but on the third, at time t+3, the agent selects
an exploratory, non-greedy action. In learning about the value of the greedy
policy at 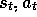 we can only use subsequent experience as long as the
greedy policy is being followed. Thus, we can use the 1-step and 2-step
returns, but not in this case the 3-step return. The n
-step returns
for all
we can only use subsequent experience as long as the
greedy policy is being followed. Thus, we can use the 1-step and 2-step
returns, but not in this case the 3-step return. The n
-step returns
for all 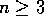 no longer have any necessary relationship to the greedy
policy.
no longer have any necessary relationship to the greedy
policy.
Thus, unlike TD(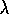 )
or Sarsa(
)
or Sarsa(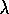 )
, Watkins's Q(
)
, Watkins's Q(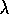 ) does not look ahead all the
way to the end of the episode in its backup. It only looks ahead
as far as the next exploratory action. Aside from this difference, however,
Watkins's Q(
) does not look ahead all the
way to the end of the episode in its backup. It only looks ahead
as far as the next exploratory action. Aside from this difference, however,
Watkins's Q(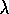 ) is much like TD(
) is much like TD(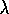 )
and Sarsa(
)
and Sarsa(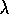 )
. Their lookahead
stops at episode's end, whereas Q(
)
. Their lookahead
stops at episode's end, whereas Q(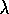 )'s lookahead stops at the first exploratory
action, or at episode's end if there are no exploratory actions before that.
Actually, to be more precise, 1-step Q-learning and Watkins's Q(
)'s lookahead stops at the first exploratory
action, or at episode's end if there are no exploratory actions before that.
Actually, to be more precise, 1-step Q-learning and Watkins's Q(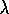 ) both look
one action past the first exploration, using their knowledge of the
action values. For example, suppose the very first action,
) both look
one action past the first exploration, using their knowledge of the
action values. For example, suppose the very first action, 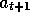 , is
exploratory. Watkins's Q(
, is
exploratory. Watkins's Q(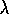 ) would still do the one step update of
) would still do the one step update of
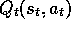 toward
toward
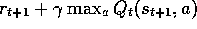 . In general, if
. In general, if 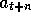 is the
first exploratory action, then the longest backup is toward:
is the
first exploratory action, then the longest backup is toward:
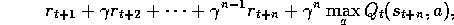
where here we assume offline
updating. The backup diagram in Figure 7.13
illustrates the forward view of Watkins's Q(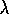 ), showing all the component
backups.
), showing all the component
backups.
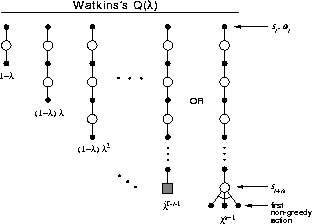
Figure 7.13: The backup diagram for Watkins's Q(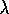 ). The series of
component backups ends with either the end of the episode or the first non-greedy
action, whichever comes first.
). The series of
component backups ends with either the end of the episode or the first non-greedy
action, whichever comes first.
The mechanistic or backward view of Watkins's Q(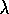 ) is also
very simple. Eligibility traces are used just as in Sarsa(
) is also
very simple. Eligibility traces are used just as in Sarsa(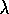 )
, except that they are
set to zero whenever an exploratory (non-greedy) action is taken. The trace
update is best thought of as occurring in two steps. First, the traces for all
state-action pairs are either decayed by
)
, except that they are
set to zero whenever an exploratory (non-greedy) action is taken. The trace
update is best thought of as occurring in two steps. First, the traces for all
state-action pairs are either decayed by 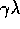 or, if an exploratory
action was taken, set to 0. Second, the trace corresponding to the current state
and action is incremented by 1. The overall result is:
or, if an exploratory
action was taken, set to 0. Second, the trace corresponding to the current state
and action is incremented by 1. The overall result is:
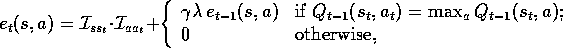
where, as before, 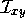 is an identity-indicator function, equal to 1 if
x=y and
0 otherwise. The rest of the algorithm is defined by:
is an identity-indicator function, equal to 1 if
x=y and
0 otherwise. The rest of the algorithm is defined by:
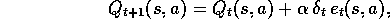
where
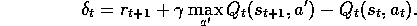
Figure 7.14 shows the complete algorithm in pseudocode.
Initializearbitrarily and
, for all s,a Repeat (for each episode): Initialize s, a Repeat (for each step of episode): Take action a, observe r,
Choose
from
using policy derived from Q (e.g.,
-greedy)
(if
ties for the max, then
)
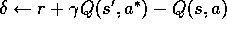
For all s,a:
If
then
else
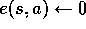
;
until s is terminal
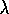 ) algorithm.
) algorithm.
Unfortunately, cutting off traces every time an exploratory action
is taken loses much of the advantage of using eligibility traces. If
exploratory actions are frequent, as they often are early in learning, then
only rarely will backups of more than one or two steps be done, and learning may
be little faster than 1-step Q-learning. Peng's Q(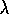 )
is an alternate version
of
Q(
)
is an alternate version
of
Q(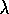 )
meant to remedy this. Peng's Q(
)
meant to remedy this. Peng's Q(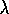 )
can be thought of as a hybrid of
Sarsa(
)
can be thought of as a hybrid of
Sarsa(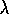 )
and Watkins's Q(
)
and Watkins's Q(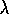 )
.
)
.
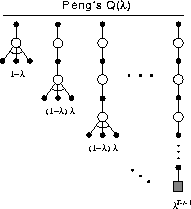
Figure 7.15: The backup diagram for Peng's Q(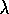 )
.
)
.
Conceptually, Peng's Q(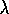 )
uses the mixture of backups shown
in Figure 7.15. Unlike Q-learning,
there is no distinction between exploratory and greedy
actions. Each component backup is over many steps of
actual experiences, and all but the last is capped by a final
maximization over actions. The component backups then are
neither on-policy nor off-policy. The earlier
transitions of each are on-policy whereas the last (fictitious)
transition uses the greedy policy. As a
consequence, for a fixed non-greedy policy,
)
uses the mixture of backups shown
in Figure 7.15. Unlike Q-learning,
there is no distinction between exploratory and greedy
actions. Each component backup is over many steps of
actual experiences, and all but the last is capped by a final
maximization over actions. The component backups then are
neither on-policy nor off-policy. The earlier
transitions of each are on-policy whereas the last (fictitious)
transition uses the greedy policy. As a
consequence, for a fixed non-greedy policy, 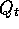 converges to neither
converges to neither 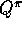 nor
nor 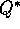 under Peng's Q(
under Peng's Q(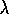 )
algorithm, but to some hybrid of the two. However, if
the policy is gradually made more greedy then the method may
still converge to
)
algorithm, but to some hybrid of the two. However, if
the policy is gradually made more greedy then the method may
still converge to 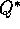 . As of this writing this has
not yet been proved. Nevertheless, the method performs
well empirically. Most studies have shown it
performing significantly better than Watkins's Q(
. As of this writing this has
not yet been proved. Nevertheless, the method performs
well empirically. Most studies have shown it
performing significantly better than Watkins's Q(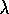 )
and
almost as well as Sarsa(
)
and
almost as well as Sarsa(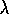 )
.
)
.
On the other hand, Peng's Q(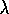 )
can not be implemented as simply as Watkins's
Q(
)
can not be implemented as simply as Watkins's
Q(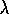 )
. For a complete description of the needed implementation, see Peng and
Williams (1994, 1996). One could
imagine yet a third version of
Q(
)
. For a complete description of the needed implementation, see Peng and
Williams (1994, 1996). One could
imagine yet a third version of
Q(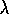 )
, let us call it naive Q (
)
, let us call it naive Q (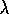 )
, that is just like Watkins's Q(
)
, that is just like Watkins's Q(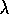 )
except
that the traces are not set to zero on exploratory actions. This method might
have some of the same advantages of Peng's Q(
)
except
that the traces are not set to zero on exploratory actions. This method might
have some of the same advantages of Peng's Q(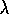 )
, but without the
complex implementation. We know of no experience with this method, but
perhaps it is not as naive as one might at first suppose.
)
, but without the
complex implementation. We know of no experience with this method, but
perhaps it is not as naive as one might at first suppose.


