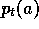A central intuition underlying reinforcement learning is that actions followed by large rewards should be made more likely to recur, whereas actions followed by small rewards should be made less likely to recur. But how is the learner to know what constitutes a large or a small reward? If an action is taken and the environment returns a reward of 5, is that large or small? To make such a judgment one must compare the reward with some standard or reference level, called the reference reward. A natural choice for the reference reward is an average of previously received rewards. In other words, a reward is interpreted as large if it is higher than average, and small if it is lower than average. Learning methods based on this idea are called reinforcement comparison methods. These methods are sometimes more effective than action-value methods. They are also the precursors to actor-critic methods, an important class of methods, which we present later, for solving the full reinforcement learning problem.
Reinforcement-comparison methods typically do not maintain estimates of action values
but only of an overall reward level. In order to pick among the actions, they
maintain a separate measure of their preference for each action. Let us denote the
preference for action a on play t by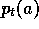 
. The preferences might be
used to determine action-selection probabilities according to a
softmax relationship, e.g.:
where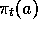 
denotes the probability of selecting action a on the tth play.
The reinforcement comparison idea is used in updating the action preferences. After
each play, the preference for the action selected on that play,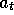 
, is incremented by
the difference between the reward,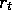 
, and the reference reward, 
:
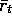where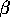 
is a positive step-size parameter. This equation implements
the idea that high rewards should increase the probability of re-selecting the
action taken and low rewards should decrease its probability.
The reference reward is an incremental average of all recently received rewards, whichever actions were taken. After the update (2.9), the reference reward is updated:
where 
, 
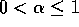, is a step size as
usual. The initial value of the reference reward,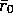 
, can be set
either optimistically, to encourage exploration, or according to prior
knowledge. The initial values of the action preferences can simply all be set to
zero. Constant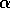 
is a good choice here
because the distribution of rewards is changing over time as action selection
improves. We see here the first case in which the learning problem is effectively
nonstationary even though the underlying problem is stationary.
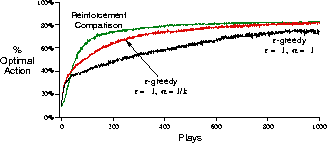
Figure 2.5: Reinforcement comparison methods versus action-value methods on the
10-armed testbed.
Reinforcement-comparison methods can be very effective, sometimes performing even
better than action-value methods. Figure 2.5 shows the
performance of the above algorithm (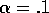
) on the 10-armed
testbed. The performances of 
-greedy (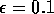
)
action-value methods with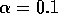 
and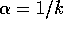 
are also shown
for comparison.
Exercise 
.
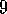
The softmax action-selection rule given for reinforcement-comparison methods
(2.8) lacks the temperature parameter, 
, used in the
earlier softmax equation (2.2). Why do you think this was done? Has any
important flexibility been lost here by omitting 
?
Exercise 
.
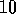
The reinforcement-comparison methods described here have two step-size parameters,
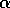and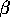 
. Could we, in general, reduce this to just one parameter by
choosing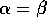 
? What would be lost by doing this?
Exercise 
.
(programming)
Suppose the initial reference reward,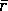 
, is far too low. Whatever action is
selected first will then probably increase in its probability of selection. Thus it
is likely to be selected again, and increased in probability again. In this way an
early action that is no better than any other could crowd out all other actions for
a long time. To counteract this effect, it is common to add a factor of
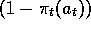to the increment in (2.9). Design and implement an
experiment to determine whether or not this really improves the performance of the
algorithm.
