


Next: 2.4 Evaluation versus Instruction
Up: 2 Evaluative Feedback
Previous: 2.2 Action-Value Methods
Although  -greedy action-selection is an effective and popular means of
balancing exploration and exploitation in reinforcement learning, one
drawback is that when it explores it chooses equally among all
actions. This means that it is just as likely to choose the worst appearing action as
it is to choose the next-to-best. In tasks where the worst actions are very
bad, this may be unsatisfactory. The obvious solution is to vary the action
probabilities as a graded function of estimated value. The greedy action is still
given the highest selection probability, but all the others are ranked and weighted
according to their value estimates. These are called softmax action
selection rules. The most common softmax method uses a Gibbs, or Boltzmann,
distribution. It chooses action a on the tth play with probability
-greedy action-selection is an effective and popular means of
balancing exploration and exploitation in reinforcement learning, one
drawback is that when it explores it chooses equally among all
actions. This means that it is just as likely to choose the worst appearing action as
it is to choose the next-to-best. In tasks where the worst actions are very
bad, this may be unsatisfactory. The obvious solution is to vary the action
probabilities as a graded function of estimated value. The greedy action is still
given the highest selection probability, but all the others are ranked and weighted
according to their value estimates. These are called softmax action
selection rules. The most common softmax method uses a Gibbs, or Boltzmann,
distribution. It chooses action a on the tth play with probability
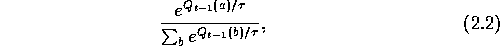
where  is a positive parameter called the temperature. High temperatures
cause the actions to be all (nearly) equi-probable. Low temperatures
cause a greater difference in selection probability for actions that differ
in their value estimates. In the limit as
is a positive parameter called the temperature. High temperatures
cause the actions to be all (nearly) equi-probable. Low temperatures
cause a greater difference in selection probability for actions that differ
in their value estimates. In the limit as 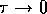 , softmax action
selection becomes the same as greedy action selection. Of course, the softmax effect
can be produced in a large number of ways other than by a Gibbs distribution. For
example, one could simply add a random number from a long-tailed distribution to each
, softmax action
selection becomes the same as greedy action selection. Of course, the softmax effect
can be produced in a large number of ways other than by a Gibbs distribution. For
example, one could simply add a random number from a long-tailed distribution to each
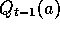 , and then pick the action whose sum was largest.
, and then pick the action whose sum was largest.
Whether softmax action selection or  -greedy action selection is better is
unclear and may depend on the task and on human factors. Both methods have only one
parameter that must be set. Most people find it easier to set the
-greedy action selection is better is
unclear and may depend on the task and on human factors. Both methods have only one
parameter that must be set. Most people find it easier to set the  \
parameter with confidence; setting
\
parameter with confidence; setting  requires knowledge of the likely action
values, and of powers of e. We know of no careful comparative studies
of these two simple action-selection rules.
requires knowledge of the likely action
values, and of powers of e. We know of no careful comparative studies
of these two simple action-selection rules.
Exercise  .
. (programming)
(programming)
How does the softmax action selection method (using the Gibbs
distribution) fare on the 10-armed testbed? Implement the
method and run it at several temperatures to produce graphs similar to
those in Figure 2.1. To verify your code, first
implement the  -greedy methods and reproduce some specific aspect of the results in
Figure 2.1.
-greedy methods and reproduce some specific aspect of the results in
Figure 2.1.
Exercise  .
. *
*
Show that in the case of two actions, the softmax operation using the Gibbs distribution
becomes the logistic, or sigmoid, function commonly used in artificial neural networks. What
effect does the temperature parameter  have on the function?
have on the function?



Next: 2.4 Evaluation versus Instruction
Up: 2 Evaluative Feedback
Previous: 2.2 Action-Value Methods
Richard Sutton
Sat May 31 12:02:11 EDT 1997
 -greedy action-selection is an effective and popular means of
balancing exploration and exploitation in reinforcement learning, one
drawback is that when it explores it chooses equally among all
actions. This means that it is just as likely to choose the worst appearing action as
it is to choose the next-to-best. In tasks where the worst actions are very
bad, this may be unsatisfactory. The obvious solution is to vary the action
probabilities as a graded function of estimated value. The greedy action is still
given the highest selection probability, but all the others are ranked and weighted
according to their value estimates. These are called softmax action
selection rules. The most common softmax method uses a Gibbs, or Boltzmann,
distribution. It chooses action a on the tth play with probability
-greedy action-selection is an effective and popular means of
balancing exploration and exploitation in reinforcement learning, one
drawback is that when it explores it chooses equally among all
actions. This means that it is just as likely to choose the worst appearing action as
it is to choose the next-to-best. In tasks where the worst actions are very
bad, this may be unsatisfactory. The obvious solution is to vary the action
probabilities as a graded function of estimated value. The greedy action is still
given the highest selection probability, but all the others are ranked and weighted
according to their value estimates. These are called softmax action
selection rules. The most common softmax method uses a Gibbs, or Boltzmann,
distribution. It chooses action a on the tth play with probability



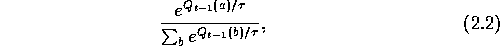
 is a positive parameter called the temperature. High temperatures
cause the actions to be all (nearly) equi-probable. Low temperatures
cause a greater difference in selection probability for actions that differ
in their value estimates. In the limit as
is a positive parameter called the temperature. High temperatures
cause the actions to be all (nearly) equi-probable. Low temperatures
cause a greater difference in selection probability for actions that differ
in their value estimates. In the limit as 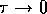 , softmax action
selection becomes the same as greedy action selection. Of course, the softmax effect
can be produced in a large number of ways other than by a Gibbs distribution. For
example, one could simply add a random number from a long-tailed distribution to each
, softmax action
selection becomes the same as greedy action selection. Of course, the softmax effect
can be produced in a large number of ways other than by a Gibbs distribution. For
example, one could simply add a random number from a long-tailed distribution to each
 , and then pick the action whose sum was largest.
, and then pick the action whose sum was largest.
 -greedy action selection is better is
unclear and may depend on the task and on human factors. Both methods have only one
parameter that must be set. Most people find it easier to set the
-greedy action selection is better is
unclear and may depend on the task and on human factors. Both methods have only one
parameter that must be set. Most people find it easier to set the  \
parameter with confidence; setting
\
parameter with confidence; setting  requires knowledge of the likely action
values, and of powers of e. We know of no careful comparative studies
of these two simple action-selection rules.
requires knowledge of the likely action
values, and of powers of e. We know of no careful comparative studies
of these two simple action-selection rules.
 .
. (programming)
(programming)
 -greedy methods and reproduce some specific aspect of the results in
Figure
-greedy methods and reproduce some specific aspect of the results in
Figure  .
. *
*
 have on the function?
have on the function?