In the previous section we presented the forward or theoretical view of the tabular
TD(![]() ) algorithm as a way of mixing backups that parametrically
shifts from a TD method to a Monte Carlo method. In this section we instead
define TD(
) algorithm as a way of mixing backups that parametrically
shifts from a TD method to a Monte Carlo method. In this section we instead
define TD(![]() ) mechanistically, and in the next section we show that this mechanism
correctly implements the forward view. The
mechanistic, or backward, view of
TD(
) mechanistically, and in the next section we show that this mechanism
correctly implements the forward view. The
mechanistic, or backward, view of
TD(![]() ) is useful because it is simple conceptually and
computationally. In particular, the forward view itself is not directly
implementable because it is acausal, using at each step knowledge of what
will happen many steps later. The backward view provides a causal, incremental
mechanism for approximating the forward view and, in the off-line case, for achieving
it exactly.
) is useful because it is simple conceptually and
computationally. In particular, the forward view itself is not directly
implementable because it is acausal, using at each step knowledge of what
will happen many steps later. The backward view provides a causal, incremental
mechanism for approximating the forward view and, in the off-line case, for achieving
it exactly.
In the backward view of TD(![]() ), there is an additional memory variable associated
with each state, its eligibility trace. The eligibility trace for state
), there is an additional memory variable associated
with each state, its eligibility trace. The eligibility trace for state ![]() at time
at time ![]() is denoted
is denoted ![]() . On each step, the eligibility traces for
all states decay by
. On each step, the eligibility traces for
all states decay by ![]() , and the eligibility trace for the one state
visited on the step is incremented by
, and the eligibility trace for the one state
visited on the step is incremented by ![]() :
:

|
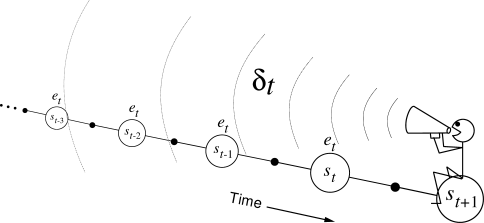
The backward view of TD(![]() ) is oriented backward in time. At
each moment we look at the current TD error and assign it backward to each
prior state according to the state's eligibility trace at
that time. We might imagine ourselves riding along the stream of states,
computing TD errors, and shouting them back to the previously visited states, as
suggested by Figure
7.8. Where the TD error and traces come
together, we get the update given by (7.7).
) is oriented backward in time. At
each moment we look at the current TD error and assign it backward to each
prior state according to the state's eligibility trace at
that time. We might imagine ourselves riding along the stream of states,
computing TD errors, and shouting them back to the previously visited states, as
suggested by Figure
7.8. Where the TD error and traces come
together, we get the update given by (7.7).
|
To better understand the backward view, consider what happens at various values
of ![]() . If
. If ![]() , then by (7.5) all traces are zero at
, then by (7.5) all traces are zero at ![]() except for
the trace corresponding to
except for
the trace corresponding to ![]() . Thus the TD(
. Thus the TD(![]() ) update (7.7) reduces
to the simple TD rule (6.2), which we henceforth call TD(0). In
terms of Figure
7.8, TD(0) is the case in which only the
one state preceding the current one is changed by the TD error. For larger
values of
) update (7.7) reduces
to the simple TD rule (6.2), which we henceforth call TD(0). In
terms of Figure
7.8, TD(0) is the case in which only the
one state preceding the current one is changed by the TD error. For larger
values of ![]() , but still
, but still ![]() , more of the preceding states are changed, but
each more temporally distant state is changed less because its eligibility
trace is smaller, as suggested in the figure. We say that the earlier states
are given less credit for the TD error.
, more of the preceding states are changed, but
each more temporally distant state is changed less because its eligibility
trace is smaller, as suggested in the figure. We say that the earlier states
are given less credit for the TD error.
If ![]() , then the credit given to earlier
states falls only by
, then the credit given to earlier
states falls only by ![]() per step. This turns out to be just the right thing to
do to achieve Monte Carlo behavior. For example, remember that the TD
error,
per step. This turns out to be just the right thing to
do to achieve Monte Carlo behavior. For example, remember that the TD
error, ![]() , includes an undiscounted term of
, includes an undiscounted term of ![]() . In passing this
back
. In passing this
back ![]() steps it needs to be discounted, like any reward in a return, by
steps it needs to be discounted, like any reward in a return, by
![]() , which is just what the falling eligibility trace achieves. If
, which is just what the falling eligibility trace achieves. If ![]() and
and ![]() , then the eligibility traces do not decay at all with time. In this case
the method behaves like a Monte Carlo method for an undiscounted, episodic
task. If
, then the eligibility traces do not decay at all with time. In this case
the method behaves like a Monte Carlo method for an undiscounted, episodic
task. If ![]() , the algorithm is also known as TD(1).
, the algorithm is also known as TD(1).
TD(1) is a way of implementing Monte Carlo algorithms that is more general than
those presented earlier and that significantly increases their range of
applicability. Whereas the earlier Monte Carlo methods were limited to episodic
tasks, TD(1) can be applied to discounted continuing tasks as well. Moreover,
TD(1) can be performed incrementally and on-line. One disadvantage of Monte Carlo
methods is that they learn nothing from an episode until it is over. For example,
if a Monte Carlo control method does something that produces a very poor reward but
does not end the episode, then the agent's tendency to do that will be
undiminished during the episode. On-line TD(1), on the other hand,
learns in an ![]() -step TD way from the incomplete ongoing episode, where the
-step TD way from the incomplete ongoing episode, where the ![]() steps are all the way up to the current step. If something unusually good or
bad happens during an episode, control methods based on TD(1) can learn
immediately and alter their behavior on that same episode.
steps are all the way up to the current step. If something unusually good or
bad happens during an episode, control methods based on TD(1) can learn
immediately and alter their behavior on that same episode.