Next: 9.5 Full vs. Sample
Up: 9 Planning and Learning
Previous: 9.3 When the Model
In the Dyna agents presented in the preceding sections, simulated transitions were
started in state-action pairs selected uniformly at random from
all previously experienced pairs. But a uniform selection is usually not the
best; planning can be much more efficient if simulated transitions and backups are
focused on particular state-action pairs.
For example, consider what happens during the second
episode of the first maze example (Figure 9.6). At the
beginning of this episode, only the state-action pair leading directly into
the goal has a positive value; the values of all other pairs are still zero. This
means that it is pointless to back up along almost all transitions, because they
take the agent from one zero-valued state to another, and thus the backups
would have no effect. Only a backup along a transition into the state just prior to
the goal, or from it into the goal, will change any values. If simulated
transitions are generated uniformly, then many wasteful backups will be made before
stumbling on one of the two useful ones. As planning progresses, the region of
useful backups grows, but planning is still far less efficient than it would be if
focused where it would do the most good. In the much larger problems that are our
real objective, the number of states is so large that an unfocused search would be
extremely inefficient.
This example suggests that search could be usefully focused by working
backward from goal states. Of course, we do not really want to use any
methods specific to the idea of ``goal state." We want methods that work for
general reward functions. Goal states are just a special case,
convenient for stimulating intuition. In general, we want to work back not
just from goal states, but from any state whose value has changed. Assume that
the values are initially correct given the model, as they were in the maze
example prior to discovering the goal. Suppose now that the agent discovers a
change in the environment and changes its estimated value of one state. Typically,
this will imply that the values of many other states should also be changed, but the
only useful 1-step backups are those of actions that lead directly into the one
state whose value has already been changed. If the values of these actions are
updated, then the values of the predecessor states may change in turn. If so, then
actions leading into them need to be backed up, and then their predecessor
states may have changed. In this way one can work backward from arbitrary states
that have changed in value, either performing useful backups or terminating the
propagation.
As the frontier of useful backups propagates backward, it often grows rapidly,
producing many state-action pairs that could usefully be backed up. But these will
not all be equally useful. The value of some states may have changed a lot, others
a little. The predecessor pairs of those that have changed a lot are more likely
to also change a lot. In a
stochastic environment, variations in estimated transition probabilities also
contribute to variations in the sizes of changes and in the urgency with which
pairs need to be backed up. It is natural to prioritize the backups according to a
measure of their urgency, and perform them in order of priority. This is the idea
behind prioritized sweeping. A queue is maintained of every
state-action pair that would change nontrivially if backed up, prioritized by the
size of the change. When the top pair in the queue is backed up, the effect on
each of its predecessor pairs is computed. If the effect is greater than some
small threshold, then the pair is inserted in the queue with the new priority (if
there is a previous entry of the pair in the queue, then insertion results in only
the higher priority entry remaining in the queue). In this way the effects of
changes are efficiently propagated backwards until quiescence. The full algorithm
for the case of deterministic environments is given in
Figure 9.9.
Initialize 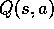 ,
, 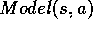 , for all s,a, and PQueue to empty
Do Forever:
(a)
, for all s,a, and PQueue to empty
Do Forever:
(a)  (b)
(b) 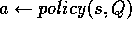 (c) Execute action a; observe resultant state,
(c) Execute action a; observe resultant state, 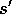 , and reward, r
(d)
, and reward, r
(d) 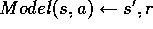 (e)
(e) 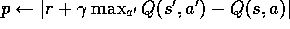 .
(f) if
.
(f) if 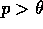 then insert s,a into PQueue with priority p
(g) Repeat N times, while PQueue is not empty:
then insert s,a into PQueue with priority p
(g) Repeat N times, while PQueue is not empty:
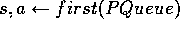
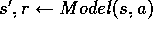
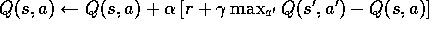 Repeat, for all
Repeat, for all 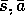 predicted to lead to s:
predicted to lead to s:

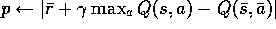 .
if
.
if 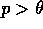 then insert
then insert 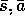 into PQueue with priority p
into PQueue with priority p
Figure 9.9: The prioritized sweeping algorithm for a deterministic environment.
Example  .
. Prioritized Sweeping on Mazes.
Prioritized sweeping has been found to dramatically increase the speed at which
optimal solutions are found in maze tasks, often by a factor of
5 to 10. A typical example is shown in Figure 9.10. These
data are for a sequence of maze tasks of
exactly the same structure as the one shown in Figure 9.5, except
varying in the grid resolution. Prioritized sweeping maintained a decisive
advantage over unprioritized Dyna-Q. Both systems made at most N=5 backups per
environmental interaction.
Prioritized Sweeping on Mazes.
Prioritized sweeping has been found to dramatically increase the speed at which
optimal solutions are found in maze tasks, often by a factor of
5 to 10. A typical example is shown in Figure 9.10. These
data are for a sequence of maze tasks of
exactly the same structure as the one shown in Figure 9.5, except
varying in the grid resolution. Prioritized sweeping maintained a decisive
advantage over unprioritized Dyna-Q. Both systems made at most N=5 backups per
environmental interaction.
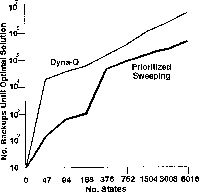
Figure 9.10: Prioritized sweeping significantly shortens learning time on
the Dyna maze task for a wide range of grid resolutions. Reprinted from Peng and
Williams (1993).

Figure 9.11: A rod maneuvering task and its solution by prioritized sweeping. The
rod must be translated and rotated around the obstacles from start to goal in
minimum number of steps. Reprinted from Moore and Atkeson (1993).
Example  .
.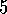 Rod Maneuvering.
The objective in this task is to maneuver a rod around some awkwardly placed
obstacles to a goal position in the fewest number of steps (Figure 9.11).
The rod can be translated along its long axis, perpendicular to that axis, or it
can be rotated in either direction around its center. The distance of
each movement was approximately 1/20th of the workspace, and the rotation increment
was 10 degrees. Translations were deterministic and quantized to one of
Rod Maneuvering.
The objective in this task is to maneuver a rod around some awkwardly placed
obstacles to a goal position in the fewest number of steps (Figure 9.11).
The rod can be translated along its long axis, perpendicular to that axis, or it
can be rotated in either direction around its center. The distance of
each movement was approximately 1/20th of the workspace, and the rotation increment
was 10 degrees. Translations were deterministic and quantized to one of 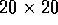 positions. The figure shows the obstacles and the shortest solution from start
to goal, found by prioritized sweeping. This problem is still deterministic, but
has 4 actions and 14,400 potential states (some of these are unreachable because of
the obstacles). This problem is probably too large to be solved with
unprioritized methods.
positions. The figure shows the obstacles and the shortest solution from start
to goal, found by prioritized sweeping. This problem is still deterministic, but
has 4 actions and 14,400 potential states (some of these are unreachable because of
the obstacles). This problem is probably too large to be solved with
unprioritized methods.
Prioritized sweeping is clearly a powerful idea, but the algorithms that
have been developed so far appear not to extend easily to more interesting cases.
The greatest problem is that the algorithms appear to rely on the assumption of
discrete states. When a change occurs at one state, these methods perform a
computation on all the predecessor states that may have been affected. If a
function approximator is used to learn the model or the value function, then a
single backup could influence a great many other states. It is not apparent how
these states could be identified or processed efficiently. On the other hand, the
general idea of focusing search on the states believed to have changed in value, and
then on their predecessors, seems intuitively to be valid in general. Additional
research may produce more general versions of prioritized sweeping.
Extensions of prioritized sweeping to stochastic environments are relatively
straightforward. The model is maintained by keeping counts of the number of times
each state-action pair has been experienced and of what the next states were. It
is natural then to backup each pair not with a sample backup, as we have been
using so far, but with a full backup, taking into account all possible next states
and their probability of occurring.



Next: 9.5 Full vs. Sample
Up: 9 Planning and Learning
Previous: 9.3 When the Model
Richard Sutton
Fri May 30 17:11:38 EDT 1997
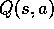 ,
, 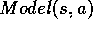 , for all s,a, and PQueue to empty
Do Forever:
(a)
, for all s,a, and PQueue to empty
Do Forever:
(a)  (b)
(b) 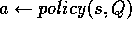 (c) Execute action a; observe resultant state,
(c) Execute action a; observe resultant state, 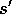 , and reward, r
(d)
, and reward, r
(d) 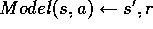 (e)
(e) 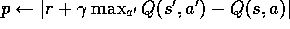 .
(f) if
.
(f) if 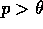 then insert s,a into PQueue with priority p
(g) Repeat N times, while PQueue is not empty:
then insert s,a into PQueue with priority p
(g) Repeat N times, while PQueue is not empty:
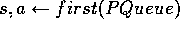
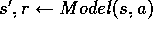
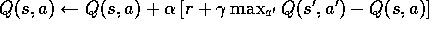 Repeat, for all
Repeat, for all 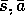 predicted to lead to s:
predicted to lead to s:

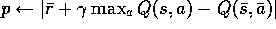 .
if
.
if 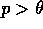 then insert
then insert 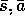 into PQueue with priority p
into PQueue with priority p



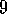 .
. Prioritized Sweeping on Mazes.
Prioritized sweeping has been found to dramatically increase the speed at which
optimal solutions are found in maze tasks, often by a factor of
5 to 10. A typical example is shown in Figure
Prioritized Sweeping on Mazes.
Prioritized sweeping has been found to dramatically increase the speed at which
optimal solutions are found in maze tasks, often by a factor of
5 to 10. A typical example is shown in Figure 


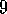 .
.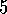 Rod Maneuvering.
The objective in this task is to maneuver a rod around some awkwardly placed
obstacles to a goal position in the fewest number of steps (Figure
Rod Maneuvering.
The objective in this task is to maneuver a rod around some awkwardly placed
obstacles to a goal position in the fewest number of steps (Figure 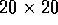 positions. The figure shows the obstacles and the shortest solution from start
to goal, found by prioritized sweeping. This problem is still deterministic, but
has 4 actions and 14,400 potential states (some of these are unreachable because of
the obstacles). This problem is probably too large to be solved with
unprioritized methods.
positions. The figure shows the obstacles and the shortest solution from start
to goal, found by prioritized sweeping. This problem is still deterministic, but
has 4 actions and 14,400 potential states (some of these are unreachable because of
the obstacles). This problem is probably too large to be solved with
unprioritized methods.