Next: 8.3.4 Kanerva Coding
Up: 8.3 Linear Methods
Previous: 8.3.2 Tile Coding
Radial basis functions (RBFs) are the natural generalization of coarse
coding to continuous-valued features. Rather than each feature being
either 0 or 1, it can be anything in the interval 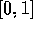 , reflecting
various degrees to which the feature is present. A typical RBF
feature,
i, has a gaussian (bell-shaped) response,
, reflecting
various degrees to which the feature is present. A typical RBF
feature,
i, has a gaussian (bell-shaped) response, 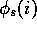 , dependent only on
the distance between the state, s, and the feature's prototypical or
center state,
, dependent only on
the distance between the state, s, and the feature's prototypical or
center state, 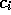 , and relative to the feature's width,
, and relative to the feature's width, 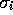 :
:
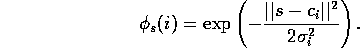
The norm or distance metric of course can be chosen in whatever way seems
most appropriate to the states and task at hand.
Figure 8.7 shows a 1-dimensional example with a euclidean distance
metric.
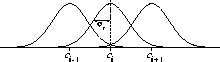
Figure 8.7: One-dimensional radial basis functions.
An RBF network is simply a linear function approximator using RBFs
for its features. Learning is defined by equations,
(8.3) and (8.8) in exactly the same way it is
for other linear function approximators. The primary advantage of
RBFs over binary features is that they produce approximate functions that vary
smoothly and are differentiable. In addition, some learning methods for
RBF networks change the centers and widths of the features as well. Such
nonlinear methods may be able to fit the target function much more precisely.
The downside to RBF networks, and to nonlinear RBF networks especially, is
greater computational complexity and, often, more manual tuning before learning
is robust and efficient.
Richard Sutton
Sat May 31 15:08:20 EDT 1997
 , reflecting
various degrees to which the feature is present. A typical RBF
feature,
i, has a gaussian (bell-shaped) response,
, reflecting
various degrees to which the feature is present. A typical RBF
feature,
i, has a gaussian (bell-shaped) response, 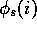 , dependent only on
the distance between the state, s, and the feature's prototypical or
center state,
, dependent only on
the distance between the state, s, and the feature's prototypical or
center state, 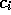 , and relative to the feature's width,
, and relative to the feature's width, 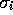 :
: