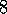 .
.



Despite our treatment of generalization and function approximation late in the book, they have always been an integral part of reinforcement learning. It is only in the last decade or less that the field has focused on the tabular case, as we have here for the first seven chapters. Bertsekas and Tsitsiklis (1996) present the state of the art in function approximation in reinforcement learning, and the collection of papers by Boyan, Moore, and Sutton (1995) is also useful. Some of the early work with function approximation in reinforcement learning is discussed at the end of this section.
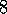 .
.
Gradient-descent methods for the minimizing mean-squared-error in supervised learning are well known. Widrow and Hoff (1960) introduced the Least-Mean-Square (LMS) algorithm, which is the prototypical incremental gradient-descent algorithm. Details of this and related algorithms are provided in many texts (e.g., Widrow and Stearns, 1985; Bishop, 1995; Duda and Hart, 1973).
Gradient-descent analyses of TD learning date back at least to Sutton (1988). Methods more sophisticated than the simple gradient-descent methods covered in this section have also been studied in the context of reinforcement learning, such as quasi-Newton methods (see Werbos, 1990) and recursive-least squares methods (Bradtke, 1993, 1994; Bradtke and Barto, 1996; Bradtke, Barto, and Ydstie, 1994). Bertsekas and Tsitsiklis (1996) provide a good discussion of these methods.
The earliest use of state aggregation in reinforcement learning may have been Michie and Chambers's (1968) BOXES system. The theory of state aggregation in reinforcement learning has been developed by Singh, Jaakkola, and Jordan (1995) and Tsitsiklis and Van Roy (1996).
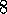 .
.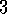
TD(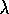 )
with linear gradient-descent function approximation was first explored by
Sutton (1988, 1984), who proved convergence of TD(0) in the mean to the minimal
MSE solution for the case in which the feature vectors,
)
with linear gradient-descent function approximation was first explored by
Sutton (1988, 1984), who proved convergence of TD(0) in the mean to the minimal
MSE solution for the case in which the feature vectors,
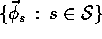 , were linearly independent. Convergence with
probability one for general
, were linearly independent. Convergence with
probability one for general 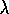 was proved by several researchers all at about
the same time (Peng, 1993; Dayan and Sejnowski, 1994; Tsitsiklis, 1994; Gurvitz,
Lin, and Hanson, 1994). Jaakkola, Jordan, and Singh (1994), in addition, proved
convergence under online updating. All of these results assumed linearly
independent features vectors, which implies at least as many component to
was proved by several researchers all at about
the same time (Peng, 1993; Dayan and Sejnowski, 1994; Tsitsiklis, 1994; Gurvitz,
Lin, and Hanson, 1994). Jaakkola, Jordan, and Singh (1994), in addition, proved
convergence under online updating. All of these results assumed linearly
independent features vectors, which implies at least as many component to 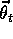 as there are states. Convergence of linear TD(
as there are states. Convergence of linear TD(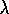 )
for the more interesting case of
general (dependent) feature vectors was first shown by Dayan (1992). A
significant generalization and strengthening of Dayan's result was proved by
Tsitsiklis and Van Roy (1997). They proved the
main presented in Section 8.2, the bound on the asymptotic error of TD(
)
for the more interesting case of
general (dependent) feature vectors was first shown by Dayan (1992). A
significant generalization and strengthening of Dayan's result was proved by
Tsitsiklis and Van Roy (1997). They proved the
main presented in Section 8.2, the bound on the asymptotic error of TD(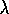 )
and
other bootstrapping methods.
)
and
other bootstrapping methods.
Our presentation of the range of possibilities for linear function approximators is based on that by Barto (1990). The term coarse coding is due to Hinton (1984), and our Figure 8.2 is based on one of his figures. Waltz and Fu (1965) provide an early example of this type of function approximation in a reinforcement learning system.
Tile coding, including hashing, was introduced by Albus (1971, 1981). He described it in terms of his ``cerebellar model articulator controller," or CMAC, as tile coding is known in the literature. The term ``tile coding" is new to this book, though the idea of describing CMAC in these terms is taken from Watkins (1989). Tile coding has been used in many reinforcement learning systems (e.g., Shewchuk and Dean, 1990; Lin and Kim, 1991; Miller, 1994; Sofge and White, 1992; Tham, 1994; Sutton, 1996; Watkins, 1989) as well as in other types of learning control systems (e.g., Kraft and Campagna, 1990; Kraft, Miller, and Dietz, 1992).
Function approximation using radial basis functions (RBFs) has received wide attention ever since being related to neural networks by Broomhead and Lowe (1988). Powell (1987) reviewed earlier uses of RBFs, and Poggio and Girosi (1989, 1990) extensively developed and applied this approach.
What we call ``Kanerva coding" was introduced by Kanerva (1988), as part of his more general idea of sparse distributed memory. A good review of this and related memory models is provided by Kanerva (1993). This approach has been pursued by Gallant (1993) and by Sutton and Whitehead (1993), among others.
 .
.
Q(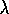 )
with function approximation was first explored by Watkins (1989).
Sarsa(
)
with function approximation was first explored by Watkins (1989).
Sarsa(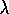 )
with function approximation was first explored by Rummery and Niranjan
(1994). The mountain-car example is based on a similar
task studied by Moore (1990). The results on it presented
here are from Sutton (1995) and Singh and Sutton (1996).
)
with function approximation was first explored by Rummery and Niranjan
(1994). The mountain-car example is based on a similar
task studied by Moore (1990). The results on it presented
here are from Sutton (1995) and Singh and Sutton (1996).
Convergence of the control methods presented in this section has not been proven
(and seems unlikely for Q(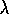 )
given the results presented in the next section).
Convergence results for control methods with state-aggregation and other
special-case function approximators are proved by Tsitsiklis and Van Roy (1996),
Singh, Jaakkola and Jordan (1995), and Gordon
(1995).
)
given the results presented in the next section).
Convergence results for control methods with state-aggregation and other
special-case function approximators are proved by Tsitsiklis and Van Roy (1996),
Singh, Jaakkola and Jordan (1995), and Gordon
(1995).
 .
.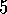
Baird's counterexample is due to Baird (1995). Tsitsiklis and Van Roy's counterexample is due to Tsitsiklis and Van Roy (1997). Averaging function approximators are developed by Gordon (1995, 1996). Gradient-descent methods for minimizing the Bellman error are due to Baird, who calls them residual-gradient methods. Other examples of instability with off-policy DP methods and more complex function approximators are given by Boyan and Moore (1995). Bradtke (1993) gives an example in which Q-learning using linear function approximation in a linear quadratic regulation problem can converge to a destabilizing policy.
The use of function approximation in reinforcement learning goes back to the early neural networks of Farley and Clark (1954; Clark and Farley, 1955), who used reinforcement learning to adjust the parameters of linear threshold functions representing policies. The earliest example we know of in which function approximation methods were used for learning value functions was Samuel's checkers player (1959, 1967). Samuel followed Shannon's (1950b) suggestion that a value function did not have to be exact to be a useful guide to selecting moves in a game and that it might be approximated by linear combination of features. In addition to linear function approximation, Samuel also experimented with lookup tables and hierarchical lookup tables called signature tables (Griffith, 1966, 1974; Page, 1977; Biermann, Fairfield, and Beres, 1982).
At about the same time as Samuel's work, Bellman and Dreyfus (1959) proposed using function approximation methods with DP. (It is tempting to think that Bellman and Samuel had some influence on one another, but we know of no reference to the other in the work of either.) There is now a fairly extensive literature on function approximation methods and DP, such as multigrid methods and methods using splines and orthogonal polynomials (e.g., Bellman and Dreyfus, 1959; Bellman, Kalaba, and Kotkin, 1973; Daniel, 1976; Whitt, 1978; Reetz, 1977; Schweitzer and Seidmann, 1985; Chow and Tsitsiklis, 1991; Kushner and Dupuis, 1992; Rust, 1996).
Holland's (1986) classifier system used a selective feature match technique to generalize evaluation information across state-action pairs. Each classifier matched a subset of states having specified values for a subset of features, with the remaining features having arbitrary values (``wild cards"). These subsets were then used in a conventional state-aggregation approach to function approximation. Holland's idea was to use a genetic algorithm to evolve a set of classifiers that collectively would implement a useful action-value function. Holland's ideas influenced the early research of the authors on reinforcement learning, but we focused on different approaches to function approximation. As function approximators, classifiers are limited in several ways. First, they are state-aggregation methods, with concomitant limitations in scaling and in representing smooth functions efficiently. In addition, the matching rules of classifiers can implement only aggregation boundaries that are parallel to the feature axes. Perhaps the most important limitation of conventional classifier systems is that the classifiers are learned via the genetic algorithm, an evolutionary method. As we discussed in Chapter 1, there is available during learning much more detailed information about how to learn than can be used by evolutionary methods. This perspective led us to instead adapt supervised-learning methods for use in reinforcement learning, specifically gradient-descent and neural-network methods. These differences between Holland's approach and ours are not surprising because Holland's ideas were developed during a period when neural networks were generally regarded as being too weak in computational power to be useful, whereas our work was at the beginning of the period that saw widespread questioning of that conventional wisdom. There remain many opportunities for combining aspects of these different approaches.
A number of reinforcement learning studies using function
approximation methods that we have not covered previously should be
mentioned. Barto, Sutton and Brouwer
(1981) and Barto and Sutton (1981) extended
the idea of an associative memory network (e.g., Kohonen, 1977; Anderson,
Silverstein, Ritz, and Jones,
1977) to reinforcement
learning. Hampson (1983, 1989) was an early
proponent of multi-layer neural networks for learning value functions. Anderson
(1986, 1987) coupled a TD algorithm with the
error backpropagation algorithm to learn a value function. Barto and Anandan
(1985) introduced a stochastic version of Widrow, Gupta, and
Maitra's (1973) selective bootstrap algorithm, which
they called the associative reward-penalty (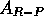 ) algorithm.
Williams (1986, 1987, 1988,
1992) extended
this type of algorithm to a general class of ``REINFORCE" algorithms, showing
that they perform stochastic gradient ascent on the expected reinforcement.
Gullapalli (1990) and Williams devised algorithms for learning
generalizing policies for the case of continuous actions. Phansalkar and
Thathachar (1995) proved both local and global
convergence theorems for modified versions of REINFORCE algorithms. Christensen
and Korf (1986) experimented with regression methods for
modifying coefficients of linear value function approximations in the game of
chess. Chapman and Kaelbling (1991) and Tan
(1991) adapted decision-tree methods for learning value
functions. Explanation-based learning methods have also been adapted for
learning value functions, yielding compact representations (Yee, Saxena, Utgoff,
and Barto, 1990; Dietterich and
Flann, 1995).
) algorithm.
Williams (1986, 1987, 1988,
1992) extended
this type of algorithm to a general class of ``REINFORCE" algorithms, showing
that they perform stochastic gradient ascent on the expected reinforcement.
Gullapalli (1990) and Williams devised algorithms for learning
generalizing policies for the case of continuous actions. Phansalkar and
Thathachar (1995) proved both local and global
convergence theorems for modified versions of REINFORCE algorithms. Christensen
and Korf (1986) experimented with regression methods for
modifying coefficients of linear value function approximations in the game of
chess. Chapman and Kaelbling (1991) and Tan
(1991) adapted decision-tree methods for learning value
functions. Explanation-based learning methods have also been adapted for
learning value functions, yielding compact representations (Yee, Saxena, Utgoff,
and Barto, 1990; Dietterich and
Flann, 1995).


