


Next: 8.8 Bibliographical and Historical
Up: 8 Generalization and Function
Previous: 8.6 Should We Bootstrap?
Reinforcement learning systems must be capable of generalization
if they are to be applicable to artificial intelligence or to large
engineering applications in general. To achieve this, any of a broad range of
existing methods for supervised-learning function approximation can be
used simply by treating each backup as a training example.
Gradient-descent methods, in particular, allow a natural extension to
function approximation of all the techniques developed in previous chapters,
including eligibility traces. Linear gradient-descent methods are
particularly appealing theoretically and work well in practice when provided
with appropriate features. Choosing the features is one of the most important
ways of adding prior domain knowledge to reinforcement learning systems.
Linear methods include radial basis functions, tile coding (CMAC), and
Kanerva coding. Backpropagation methods for multi-layer neural networks are
instances of nonlinear gradient-descent function approximators.
For the most part, the extension of reinforcement learning prediction and control
methods to gradient-descent forms is straightforward. However, there is an
interesting interaction between function approximation, bootstrapping, and the
on-policy/off-policy distinction. Bootstrapping methods, such as DP and
TD(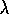 )
for
)
for 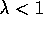 , work reliably in conjunction with function approximation over a
narrower range of conditions than non-bootstrapping methods. As the control
case has not yet yielded to theoretical analysis, research has focused on the
value prediction problem. In this case, on-policy bootstrapping methods
converge reliably with linear gradient-descent function approximators to a
solution with mean square error bounded by
, work reliably in conjunction with function approximation over a
narrower range of conditions than non-bootstrapping methods. As the control
case has not yet yielded to theoretical analysis, research has focused on the
value prediction problem. In this case, on-policy bootstrapping methods
converge reliably with linear gradient-descent function approximators to a
solution with mean square error bounded by  times
the minimum possible error. Off-policy methods, on the other hand, may diverge to
infinite error. Several approaches have been explored to making off-policy
bootstrapping methods work with function approximation, but this is still an
open research issue. Bootstrapping methods are of persistent interest in
reinforcement learning, despite their limited theoretical guarantees, because in
practice they usually work significantly better than non-bootstrapping methods.
times
the minimum possible error. Off-policy methods, on the other hand, may diverge to
infinite error. Several approaches have been explored to making off-policy
bootstrapping methods work with function approximation, but this is still an
open research issue. Bootstrapping methods are of persistent interest in
reinforcement learning, despite their limited theoretical guarantees, because in
practice they usually work significantly better than non-bootstrapping methods.



Next: 8.8 Bibliographical and Historical
Up: 8 Generalization and Function
Previous: 8.6 Should We Bootstrap?
Richard Sutton
Sat May 31 15:08:20 EDT 1997
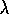 )
for
)
for 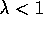 , work reliably in conjunction with function approximation over a
narrower range of conditions than non-bootstrapping methods. As the control
case has not yet yielded to theoretical analysis, research has focused on the
value prediction problem. In this case, on-policy bootstrapping methods
converge reliably with linear gradient-descent function approximators to a
solution with mean square error bounded by
, work reliably in conjunction with function approximation over a
narrower range of conditions than non-bootstrapping methods. As the control
case has not yet yielded to theoretical analysis, research has focused on the
value prediction problem. In this case, on-policy bootstrapping methods
converge reliably with linear gradient-descent function approximators to a
solution with mean square error bounded by  times
the minimum possible error. Off-policy methods, on the other hand, may diverge to
infinite error. Several approaches have been explored to making off-policy
bootstrapping methods work with function approximation, but this is still an
open research issue. Bootstrapping methods are of persistent interest in
reinforcement learning, despite their limited theoretical guarantees, because in
practice they usually work significantly better than non-bootstrapping methods.
times
the minimum possible error. Off-policy methods, on the other hand, may diverge to
infinite error. Several approaches have been explored to making off-policy
bootstrapping methods work with function approximation, but this is still an
open research issue. Bootstrapping methods are of persistent interest in
reinforcement learning, despite their limited theoretical guarantees, because in
practice they usually work significantly better than non-bootstrapping methods.


