


Next: 7.4 Equivalence of the
Up: 7 Eligibility Traces
Previous: 7.2 The Forward View
In the previous section we presented the forward or theoretical view of the tabular
TD(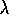 )
algorithm as a way of mixing backups that parametricaly
shifts from a TD method to a Monte Carlo method. In this section we instead
define TD(
)
algorithm as a way of mixing backups that parametricaly
shifts from a TD method to a Monte Carlo method. In this section we instead
define TD(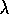 )
mechanistically, and in the next section we show that this mechanism
correctly implements the theoretical result described by the forward view. The
mechanistic, or backward, view of
TD(
)
mechanistically, and in the next section we show that this mechanism
correctly implements the theoretical result described by the forward view. The
mechanistic, or backward, view of
TD(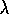 )
is useful because it is simple conceptually and
computationally. In particular, the forward view itself is not directly
implementable because it is acausal, using at each step knowledge of what
will happen many steps later. The backwards view provides a causal, incremental
mechanism for approximating the forward view, and, in the offline case, for
exactly achieving it.
)
is useful because it is simple conceptually and
computationally. In particular, the forward view itself is not directly
implementable because it is acausal, using at each step knowledge of what
will happen many steps later. The backwards view provides a causal, incremental
mechanism for approximating the forward view, and, in the offline case, for
exactly achieving it.
In the backward view of TD(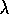 )
, there is an additional memory variable associated
with each state, its eligibility trace. The eligibility trace for state s
at time t is denoted
)
, there is an additional memory variable associated
with each state, its eligibility trace. The eligibility trace for state s
at time t is denoted 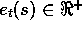 . On each step, the eligibility traces for
all states decay by
. On each step, the eligibility traces for
all states decay by 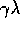 , and the eligibility trace for the one state
visited on the step is incremented by 1:
, and the eligibility trace for the one state
visited on the step is incremented by 1:
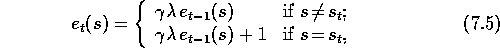
for all nonterminal states s, where 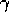 is the discount rate and
is the discount rate and
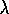 is the parameter introduced in the previous section. Henceforth we
refer to
is the parameter introduced in the previous section. Henceforth we
refer to 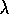 as the trace-decay parameter. This kind of eligibility trace
is called an accumulating trace because it accumulates each time the state
is visited, then fades away gradually when the state is not visited, as illustrated
below:
as the trace-decay parameter. This kind of eligibility trace
is called an accumulating trace because it accumulates each time the state
is visited, then fades away gradually when the state is not visited, as illustrated
below:

At any time, the traces record which states have recently been
visited, where ``recently" is defined in terms of 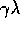 . The traces
are said to indicate the degree to which each state is eligible for
undergoing learning changes should a reinforcing event occur. The reinforcing
events we are concerned with are the moment-by-moment 1-step TD errors, e.g., for
the prediction problem:
. The traces
are said to indicate the degree to which each state is eligible for
undergoing learning changes should a reinforcing event occur. The reinforcing
events we are concerned with are the moment-by-moment 1-step TD errors, e.g., for
the prediction problem:
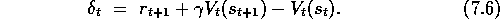
In the backward view of TD(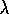 )
, the global TD error signal triggers proportional
updates to all recently visited states, as signaled by their non-zero traces:
)
, the global TD error signal triggers proportional
updates to all recently visited states, as signaled by their non-zero traces:

As always, these increments could be done on each step to form an online
algorithm, or saved until the end of the episode to produce an offline algorithm.
In either case, equations (7.5--7.7) provide the mechanistic
definition of the TD(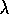 )
algorithm. A complete algorithm for online
TD(
)
algorithm. A complete algorithm for online
TD(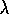 )
is given in Figure 7.7.
)
is given in Figure 7.7.
Initialize 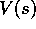 arbitrarily and
arbitrarily and 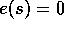 , for all
, for all 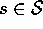 Repeat (for each episode):
Initialize s
Repeat (for each step of episode):
Repeat (for each episode):
Initialize s
Repeat (for each step of episode):
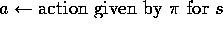 Take action a, observe reward, r, and next state,
Take action a, observe reward, r, and next state, 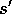
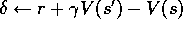
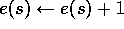 For all s:
For all s:
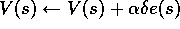
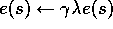
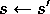 until s is terminal
until s is terminal
Figure 7.7: Online Tabular TD(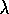 )
for estimating
)
for estimating 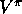 .
.
The backward view of TD(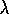 )
is oriented toward looking backward in time. At
each moment we look at the current TD error and assign it backward to each
prior state according to the state's eligibility trace at
that time. We might imagine ourselves riding along the stream of states,
computing TD errors, and shouting them back to the previously visited states, as
suggested by Figure 7.8. Where the TD error and traces come
together we get the update given by (7.7).
)
is oriented toward looking backward in time. At
each moment we look at the current TD error and assign it backward to each
prior state according to the state's eligibility trace at
that time. We might imagine ourselves riding along the stream of states,
computing TD errors, and shouting them back to the previously visited states, as
suggested by Figure 7.8. Where the TD error and traces come
together we get the update given by (7.7).
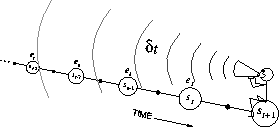
Figure 7.8: The backward or mechanistic view.
To better understand the backward view, consider what happens at various values
of 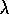 . If
. If 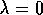 , then by (7.5) all traces are zero at t except for
the trace corresponding to
, then by (7.5) all traces are zero at t except for
the trace corresponding to 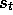 . Thus the TD(
. Thus the TD(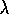 )
update (7.7) reduces
to the simple TD rule (6 .2
), which we henceforth call TD(0). In
terms of Figure 7.8, TD(0) is the case in which only the
one state preceding the current one is changed by the TD error. For larger
values of
)
update (7.7) reduces
to the simple TD rule (6 .2
), which we henceforth call TD(0). In
terms of Figure 7.8, TD(0) is the case in which only the
one state preceding the current one is changed by the TD error. For larger
values of 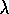 , but still
, but still 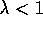 , more of the preceding states are changed, but
each more temporally distant state is changed less because its eligibility
trace is smaller, as suggested in the figure. We say that the earlier states
are given less credit for the TD error.
, more of the preceding states are changed, but
each more temporally distant state is changed less because its eligibility
trace is smaller, as suggested in the figure. We say that the earlier states
are given less credit for the TD error.
If 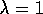 , then the credit given to earlier
states falls only by
, then the credit given to earlier
states falls only by 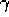 per step. This turns out to be just the right thing to
do to achieve Monte Carlo behavior. For example, remember that the TD
error,
per step. This turns out to be just the right thing to
do to achieve Monte Carlo behavior. For example, remember that the TD
error, 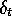 , includes an undiscounted term of
, includes an undiscounted term of 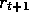 . In passing this
back k steps it needs to be discounted, just like any reward in a return, by
. In passing this
back k steps it needs to be discounted, just like any reward in a return, by
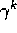 , which is just what the falling eligibility trace achieves. If both
, which is just what the falling eligibility trace achieves. If both 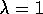 and
and 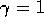 , then the eligibility traces do not decay at all with time. This turns
out to work just fine, behaving like a Monte Carlo method for an undiscounted,
episodic task. If
, then the eligibility traces do not decay at all with time. This turns
out to work just fine, behaving like a Monte Carlo method for an undiscounted,
episodic task. If 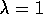 , the algorithm is also known as TD(1).
, the algorithm is also known as TD(1).
TD(1) is a way of implementing Monte Carlo algorithms that is more general than
those presented earlier and that significantly increases their range of
applicability. Whereas the earlier Monte Carlo methods were limited to episodic
tasks, TD(1) can be applied to discounted continuing tasks as well. Moreover,
TD(1) can be performed incrementally and online. One disadvantage of Monte Carlo
methods is that they learn nothing from an episode until it is over. For example,
if something a Monte Carlo control method does produces a very poor reward, but
does not end the episode, then the agent's tendency to do that will be
undiminished during that episode. Online TD(1), on the other hand,
learns in an n
-step TD way from the incomplete ongoing episode, where the n
\
steps are all the way up to the current step. If something unusually good or
bad happens during an episode, control methods based on TD(1) can learn
immediately and alter their behavior on that same episode.



Next: 7.4 Equivalence of the
Up: 7 Eligibility Traces
Previous: 7.2 The Forward View
Richard Sutton
Fri May 30 15:01:47 EDT 1997
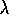 )
algorithm as a way of mixing backups that parametricaly
shifts from a TD method to a Monte Carlo method. In this section we instead
define TD(
)
algorithm as a way of mixing backups that parametricaly
shifts from a TD method to a Monte Carlo method. In this section we instead
define TD(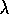 )
mechanistically, and in the next section we show that this mechanism
correctly implements the theoretical result described by the forward view. The
mechanistic, or backward, view of
TD(
)
mechanistically, and in the next section we show that this mechanism
correctly implements the theoretical result described by the forward view. The
mechanistic, or backward, view of
TD(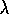 )
is useful because it is simple conceptually and
computationally. In particular, the forward view itself is not directly
implementable because it is acausal, using at each step knowledge of what
will happen many steps later. The backwards view provides a causal, incremental
mechanism for approximating the forward view, and, in the offline case, for
exactly achieving it.
)
is useful because it is simple conceptually and
computationally. In particular, the forward view itself is not directly
implementable because it is acausal, using at each step knowledge of what
will happen many steps later. The backwards view provides a causal, incremental
mechanism for approximating the forward view, and, in the offline case, for
exactly achieving it.



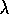 )
, there is an additional memory variable associated
with each state, its eligibility trace. The eligibility trace for state s
at time t is denoted
)
, there is an additional memory variable associated
with each state, its eligibility trace. The eligibility trace for state s
at time t is denoted 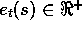 . On each step, the eligibility traces for
all states decay by
. On each step, the eligibility traces for
all states decay by 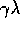 , and the eligibility trace for the one state
visited on the step is incremented by 1:
, and the eligibility trace for the one state
visited on the step is incremented by 1:
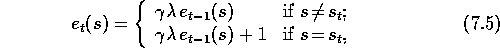
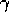 is the discount rate and
is the discount rate and
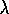 is the parameter introduced in the previous section. Henceforth we
refer to
is the parameter introduced in the previous section. Henceforth we
refer to 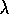 as the trace-decay parameter. This kind of eligibility trace
is called an accumulating trace because it accumulates each time the state
is visited, then fades away gradually when the state is not visited, as illustrated
below:
as the trace-decay parameter. This kind of eligibility trace
is called an accumulating trace because it accumulates each time the state
is visited, then fades away gradually when the state is not visited, as illustrated
below:

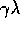 . The traces
are said to indicate the degree to which each state is eligible for
undergoing learning changes should a reinforcing event occur. The reinforcing
events we are concerned with are the moment-by-moment 1-step TD errors, e.g., for
the prediction problem:
. The traces
are said to indicate the degree to which each state is eligible for
undergoing learning changes should a reinforcing event occur. The reinforcing
events we are concerned with are the moment-by-moment 1-step TD errors, e.g., for
the prediction problem:
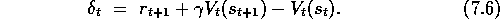
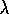 )
, the global TD error signal triggers proportional
updates to all recently visited states, as signaled by their non-zero traces:
)
, the global TD error signal triggers proportional
updates to all recently visited states, as signaled by their non-zero traces:

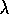 )
algorithm. A complete algorithm for online
TD(
)
algorithm. A complete algorithm for online
TD(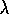 )
is given in Figure
)
is given in Figure 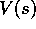 arbitrarily and
arbitrarily and 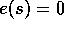 , for all
, for all 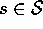 Repeat (for each episode):
Initialize s
Repeat (for each step of episode):
Repeat (for each episode):
Initialize s
Repeat (for each step of episode):
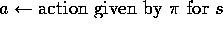 Take action a, observe reward, r, and next state,
Take action a, observe reward, r, and next state, 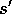
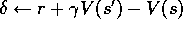
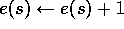 For all s:
For all s:
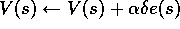
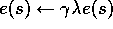
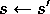 until s is terminal
until s is terminal
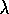 )
for estimating
)
for estimating 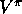 .
.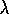 )
is oriented toward looking backward in time. At
each moment we look at the current TD error and assign it backward to each
prior state according to the state's eligibility trace at
that time. We might imagine ourselves riding along the stream of states,
computing TD errors, and shouting them back to the previously visited states, as
suggested by Figure
)
is oriented toward looking backward in time. At
each moment we look at the current TD error and assign it backward to each
prior state according to the state's eligibility trace at
that time. We might imagine ourselves riding along the stream of states,
computing TD errors, and shouting them back to the previously visited states, as
suggested by Figure 
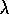 . If
. If 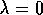 , then by (
, then by (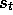 . Thus the TD(
. Thus the TD(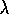 )
update (
)
update (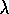 , but still
, but still 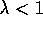 , more of the preceding states are changed, but
each more temporally distant state is changed less because its eligibility
trace is smaller, as suggested in the figure. We say that the earlier states
are given less credit for the TD error.
, more of the preceding states are changed, but
each more temporally distant state is changed less because its eligibility
trace is smaller, as suggested in the figure. We say that the earlier states
are given less credit for the TD error.
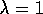 , then the credit given to earlier
states falls only by
, then the credit given to earlier
states falls only by 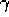 per step. This turns out to be just the right thing to
do to achieve Monte Carlo behavior. For example, remember that the TD
error,
per step. This turns out to be just the right thing to
do to achieve Monte Carlo behavior. For example, remember that the TD
error, 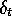 , includes an undiscounted term of
, includes an undiscounted term of 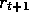 . In passing this
back k steps it needs to be discounted, just like any reward in a return, by
. In passing this
back k steps it needs to be discounted, just like any reward in a return, by
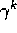 , which is just what the falling eligibility trace achieves. If both
, which is just what the falling eligibility trace achieves. If both 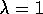 and
and 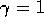 , then the eligibility traces do not decay at all with time. This turns
out to work just fine, behaving like a Monte Carlo method for an undiscounted,
episodic task. If
, then the eligibility traces do not decay at all with time. This turns
out to work just fine, behaving like a Monte Carlo method for an undiscounted,
episodic task. If 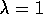 , the algorithm is also known as TD(1).
, the algorithm is also known as TD(1).