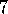 .
. and 7
.2
and 7
.2



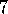 .
. and 7
.2
and 7
.2
The forward view of eligibility traces in terms of n
-step returns and the
 -return is due to Watkins (1989), who also first discussed the error-correction
property of n
-step returns. Our presentation is based on the slightly modified
treatment by Jaakkola, Jordan, and Singh (1994). The results in the random-walk
examples were made for this text based on the prior work by Sutton (1988) and
Singh and
Sutton (1996). The use of backup diagrams to describe these and other
algorithms in this chapter is new, as are the terms ``forward view" and ``backward
view."
-return is due to Watkins (1989), who also first discussed the error-correction
property of n
-step returns. Our presentation is based on the slightly modified
treatment by Jaakkola, Jordan, and Singh (1994). The results in the random-walk
examples were made for this text based on the prior work by Sutton (1988) and
Singh and
Sutton (1996). The use of backup diagrams to describe these and other
algorithms in this chapter is new, as are the terms ``forward view" and ``backward
view."
TD(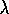 )
was proved to converge in the mean by Dayan (1992), and with
probability one by many researchers, including Peng (1993), Dayan and
Sejnowski (1994), and Tsitsiklis
(1994).
Jaakkola, Jordan and Singh (1994) in addition
first proved convergence of
TD(
)
was proved to converge in the mean by Dayan (1992), and with
probability one by many researchers, including Peng (1993), Dayan and
Sejnowski (1994), and Tsitsiklis
(1994).
Jaakkola, Jordan and Singh (1994) in addition
first proved convergence of
TD(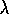 )
under online updating. Gurvits, Lin, and Hanson
(1994) proved convergence of a more general class
of eligibility-trace methods.
)
under online updating. Gurvits, Lin, and Hanson
(1994) proved convergence of a more general class
of eligibility-trace methods.
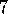 .
.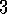
The idea that stimuli produce aftereffects in the nervous system that are
important for learning is very old. Animal learning psychologists at least as
far back as Pavlov (1927) and Hull (1943, 1952) included such ideas in their
theories. However, stimulus traces in these
theories are more like transient state representations than what we are calling
eligibility traces: they could be associated with actions, whereas an eligibility
trace is used only for credit assignment. The idea of a stimulus trace serving
exclusively for credit assignment is apparently due to Klopf
(1972), who proposed that a neuron's synapses become
``eligible" under certain conditions for modification if, and when,
reinforcement arrives later at the neuron. Our subsequent use of eligibility
traces was based on Klopf's work (Sutton, 1978; Barto and Sutton, 1981;
Sutton and Barto, 1981; Barto, Sutton, and Anderson, 1983; Sutton, 1984). The
TD(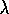 )
algorithm itself is due to Sutton (1988).
)
algorithm itself is due to Sutton (1988).
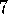 .
.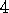
The equivalence of forward and backwards views, and the relationships to Monte Carlo methods, were developed by Sutton (1988) for undiscounted episodic tasks, then extended by Watkins to the general case. The idea in exercise 7.5 is new.
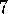 .
.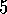
Sarsa(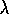 )
was first explored as a control method by Rummery and Niranjan
(1994) and Rummery (1995).
)
was first explored as a control method by Rummery and Niranjan
(1994) and Rummery (1995).
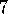 .
.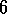
Watkins's Q(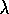 )
is due to Watkins (1989). Peng's Q(
)
is due to Watkins (1989). Peng's Q(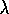 )
is due to Peng
and Williams (Peng, 1993; Peng and Williams, 1994,
1996). Rummery
(1995) made extensive comparative studies of these
algorithms.
)
is due to Peng
and Williams (Peng, 1993; Peng and Williams, 1994,
1996). Rummery
(1995) made extensive comparative studies of these
algorithms.
Convergence has not been proved for any control method for 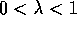 .
.
 .
.
Actor-critic methods were among the first to use eligibility traces (Barto, Sutton and Anderson, 1983; Sutton, 1984). The specific algorithm discussed in this chapter has never been tried before.
 .
.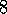
Replacing traces are due to Singh and Sutton (1996). The results in Figure 7.17 are from their paper. The task in the example of this section was first used to show the weakness of accumulating traces by Sutton (1984). The relationship of both kinds of traces to specific Monte Carlo methods were developed by Singh and Sutton (1996).
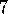 .
.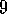 and 7
.10
and 7
.10
The ideas in these two sections were generally known for many years, but, beyond
what is in the sources cited in the sections themselves, this text may be the first
place they have been described. Perhaps the first published discussion of
variable 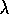 was by Watkins (1989), who pointed out that the cutting
off of the backup sequence (Figure 7.13) in his Q(
was by Watkins (1989), who pointed out that the cutting
off of the backup sequence (Figure 7.13) in his Q(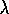 )
when
a non-greedy action was selected could be implemented by temporarily setting
)
when
a non-greedy action was selected could be implemented by temporarily setting
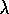 to 0.
to 0.


