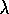Eligibility traces in conjunction with TD errors provide an efficient,
incremental way of shifting and choosing between Monte Carlo and TD
methods. Traces can be used without TD errors to achieve a similar
effect, but only awkwardly. A method such as TD(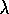
)
enables this to be
done from partial experiences and with little memory and little
non-meaningful variation in predictions.
As we discussed in Chapter 5 , Monte Carlo methods have advantages in tasks in which the state is not completely known and which thus appear to be non-Markov. Because eligibility traces make TD methods more like Monte Carlo methods, they also have advantages in these cases. If one wants to use TD methods because of their other advantages, but the task is at least partially non-Markov, then the use of an eligibility-trace method is indicated. Eligibility traces are the first line of defense against both long delayed rewards and non-Markov tasks.
By adjusting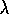 
, we can place eligibility-trace methods anywhere along
a continuum from Monte Carlo and TD methods. Where shall we place them? We do
not yet have a good theoretical answer to this question, but a clear empirical
answer appears to be emerging. On tasks with many steps per episode, or many
steps within the half-life of discounting, then it appears significantly better to
use eligibility traces than not to (e.g., see Figure 8 .10
). On the
other hand, if the traces are so long as to produce a pure Monte Carlo method, or
nearly so, then performance again degrades sharply. An intermediate mixture
appears the best choice. Eligibility traces should be used to bring us toward
Monte Carlo methods, but not all the way there. In the future it may be possible
to vary the tradeoff between TD and Monte Carlo methods more finely using variable
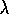, but at present it is not clear how this can be done reliably and usefully.
Methods using eligibility traces require more computation than 1-step methods, but in return they offer significantly faster learning, particularly when rewards are delayed by many steps. Thus it often makes sense to use eligibility traces when data is scarce and can not be repeatedly processed, as is often the case in online applications. On the other hand, in offline applications in which data can be generated cheaply, perhaps from an inexpensive simulation, then it often does not pay to use eligibility traces. In these cases the objective is not to get more out of a limited amount of data, but simply to process as much data as quickly as possible. In these cases the speedup per datum due to traces is typically not worth their computational cost, and 1-step methods are favored.