Next: 3.9 Optimality and Approximation
Up: 3 The Reinforcement Learning
Previous: 3.7 Value Functions
Solving a reinforcement learning task means, roughly, finding a policy that
achieves a lot of reward over the long run. For finite
MDPs, we can precisely define an optimal policy in the following way.
Value functions define a partial ordering over policies. A policy  is defined to be better than or equal to a policy
is defined to be better than or equal to a policy 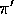 if its expected return
is greater than or equal to that of
if its expected return
is greater than or equal to that of 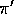 for all states. In other words,
for all states. In other words,
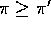 if and only if
if and only if
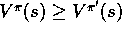 for all
for all 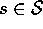 . There is always at least one
policy that is better than or equal to all other policies. This is an
optimal policy. Although there may be more than one, we denote all the optimal
policies by
. There is always at least one
policy that is better than or equal to all other policies. This is an
optimal policy. Although there may be more than one, we denote all the optimal
policies by 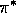 . They share the same value function, called the
optimal value function, denoted
. They share the same value function, called the
optimal value function, denoted
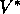 , defined as
, defined as
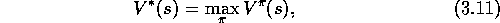
for all 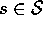 .
.
Optimal policies also share the same optimal action-value function,
denoted
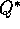 , defined as
, defined as
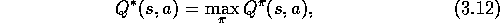
for all 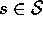 and
and 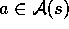 .
For state-action pair
.
For state-action pair 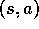 , this function gives the expected return for
taking action a in state s and thereafter following an optimal policy.
Thus, we can write
, this function gives the expected return for
taking action a in state s and thereafter following an optimal policy.
Thus, we can write 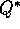 in terms of
in terms of 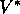 as follows:
as follows:
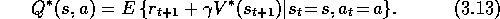
Example  .
. Optimal Value Functions for Golf.
The lower part of Figure 3.6 shows the contours of a possible optimal
action-value function
Optimal Value Functions for Golf.
The lower part of Figure 3.6 shows the contours of a possible optimal
action-value function 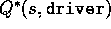 . These are the values of each
state if we first play a stroke with the driver and then afterwards select either the
driver or the putter, whichever is best. The driver enables us to hit the ball
farther, but with less accuracy. We can reach the hole in one shot using the
driver only if we are already very close; thus the -1 contour for
. These are the values of each
state if we first play a stroke with the driver and then afterwards select either the
driver or the putter, whichever is best. The driver enables us to hit the ball
farther, but with less accuracy. We can reach the hole in one shot using the
driver only if we are already very close; thus the -1 contour for 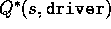 covers only a small portion of the green. If we have two strokes,
however, then we can reach the hole from much farther away, as shown by the
-2 contour. In this case we don't have to drive all the way to within the small
-1 contour, but only to anywhere on the green; from there we can use the putter.
The optimal action-value function gives the values after committing to a
particular first action, in this case, to the driver, but afterwards using
whichever actions are best. The -3 contour is still farther out and includes the
starting tee. From the tee, the best sequence of actions is two drives and one
putt, sinking the ball in three strokes.
covers only a small portion of the green. If we have two strokes,
however, then we can reach the hole from much farther away, as shown by the
-2 contour. In this case we don't have to drive all the way to within the small
-1 contour, but only to anywhere on the green; from there we can use the putter.
The optimal action-value function gives the values after committing to a
particular first action, in this case, to the driver, but afterwards using
whichever actions are best. The -3 contour is still farther out and includes the
starting tee. From the tee, the best sequence of actions is two drives and one
putt, sinking the ball in three strokes.
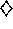
Because 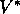 is the value function for a policy, it must satisfy the
self-consistency condition given by the Bellman equation for
state values (3.10). Because it is the optimal value function,
however,
is the value function for a policy, it must satisfy the
self-consistency condition given by the Bellman equation for
state values (3.10). Because it is the optimal value function,
however, 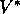 's consistency condition can be written in a special form without
reference to any specific policy. This is the Bellman equation for
's consistency condition can be written in a special form without
reference to any specific policy. This is the Bellman equation for 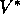 , or the
Bellman optimality equation. Intuitively,
the Bellman optimality equation expresses the fact that the value of a state under
an optimal policy must equal the expected return for the best action from that state:
, or the
Bellman optimality equation. Intuitively,
the Bellman optimality equation expresses the fact that the value of a state under
an optimal policy must equal the expected return for the best action from that state:
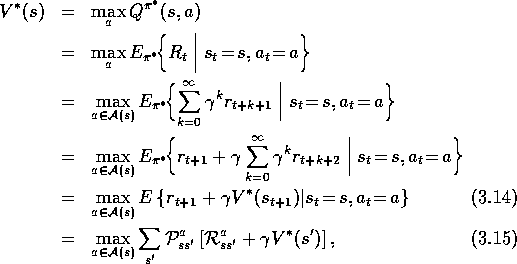
These last two equations are two forms of the Bellman optimality equation for 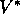 .
The Bellman optimality equation for
.
The Bellman optimality equation for 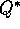 is
is
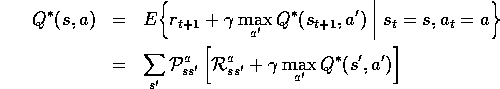
The backup diagrams in Figure 3.7 show graphically the spans of
future states and actions considered in the Bellman optimality equations for 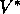 and
and
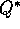 . These are the same as the backup diagrams for
. These are the same as the backup diagrams for 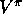 and
and 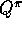 except
that arcs have been added at the agent's choice points to represent that the maximum
over that choice is taken rather than the expected value given some policy.
Figure 3.7a represents graphically the Bellman optimality equation
(3.15).
except
that arcs have been added at the agent's choice points to represent that the maximum
over that choice is taken rather than the expected value given some policy.
Figure 3.7a represents graphically the Bellman optimality equation
(3.15).
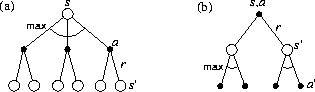
Figure 3.7: Backup diagrams for a) 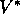 and b)
and b) 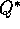
For finite MDPs, the Bellman optimality equation (3.15) has a unique
solution independent of the policy. The
Bellman optimality equation is actually a system of equations, one for each state,
so if there are N states, then there are N equations in N unknowns.
If the dynamics of the environment are known (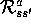 and
and 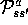 ), then
in principle one can solve this system of equations for
), then
in principle one can solve this system of equations for 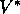 using any one of a
variety of methods for solving systems of nonlinear equations. One can solve a
related set of equations for
using any one of a
variety of methods for solving systems of nonlinear equations. One can solve a
related set of equations for
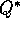 .
.
Once one has 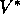 , it is relatively easy to determine an optimal policy.
For each state s, there will be one or more actions at which the maximum is obtained
in the Bellman optimality equation.
Any policy that assigns non-zero probability only to these actions is an optimal
policy. You can think of this as a one-step search. If you have the optimal value
function,
, it is relatively easy to determine an optimal policy.
For each state s, there will be one or more actions at which the maximum is obtained
in the Bellman optimality equation.
Any policy that assigns non-zero probability only to these actions is an optimal
policy. You can think of this as a one-step search. If you have the optimal value
function, 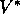 , then the actions that appear best after just a one-step search will
be optimal actions.
Another way of saying this is that any policy that is
greedy with respect to the optimal evaluation function
, then the actions that appear best after just a one-step search will
be optimal actions.
Another way of saying this is that any policy that is
greedy with respect to the optimal evaluation function 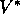 is an optimal
policy. The term greedy is used in computer science to describe any search or decision
procedure that selects alternatives based only on local or immediate considerations,
without considering the possibility that such a selection may prevent future access
to even better alternatives. Consequently, it describes policies
that select actions based only on their short-term consequences. The beauty of
is an optimal
policy. The term greedy is used in computer science to describe any search or decision
procedure that selects alternatives based only on local or immediate considerations,
without considering the possibility that such a selection may prevent future access
to even better alternatives. Consequently, it describes policies
that select actions based only on their short-term consequences. The beauty of
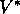 is that if one uses it to evaluate the short-term
consequences of actions, specifically, the one-step consequences, then
a greedy policy is actually optimal in the long-term sense in which we are
interested because
is that if one uses it to evaluate the short-term
consequences of actions, specifically, the one-step consequences, then
a greedy policy is actually optimal in the long-term sense in which we are
interested because 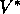 already takes into account the reward consequences of all
possible future behavior. By means of
already takes into account the reward consequences of all
possible future behavior. By means of 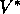 , the optimal expected long-term return is
turned into a quantity that is locally and immediately available for each state.
Hence, a one-step ahead search yields the long-term optimal actions.
, the optimal expected long-term return is
turned into a quantity that is locally and immediately available for each state.
Hence, a one-step ahead search yields the long-term optimal actions.
Having 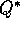 makes choosing optimal actions still
easier. With
makes choosing optimal actions still
easier. With 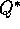 , the agent does not even have to do a one-step
ahead search: for any state s, it can simply find any action which
maximizes
, the agent does not even have to do a one-step
ahead search: for any state s, it can simply find any action which
maximizes 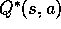 . The
action-value function effectively caches the results of all one-step ahead
searches. It provides the optimal expected long-term return as a value that is
locally and immediately available for each state-action pair. Hence, at the cost of
representing a function of state-action pairs, instead of just of states, the
optimal action value function allows optimal actions to be selected without having
to know anything about possible successor states and their values, that is, without
having to know anything about the environment's dynamics.
. The
action-value function effectively caches the results of all one-step ahead
searches. It provides the optimal expected long-term return as a value that is
locally and immediately available for each state-action pair. Hence, at the cost of
representing a function of state-action pairs, instead of just of states, the
optimal action value function allows optimal actions to be selected without having
to know anything about possible successor states and their values, that is, without
having to know anything about the environment's dynamics.
Example 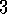 .
.
Bellman Optimality Equations for the Recycling Robot.
Using (3.15), we can explicitly give the the Bellman
optimality equation for the recycling robot example.
To make things more compact, we abbreviate the states high and low, and
the actions search, wait, and recharge respectively by h ,
l , s , w , and re . Since there are only two states, the Bellman
optimality equation consists of just two equations. The equation for 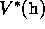 can
be written as follows:
can
be written as follows:
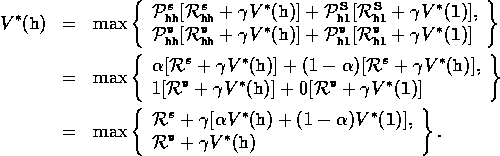
Following the same procedure for  yields the equation:
yields the equation:
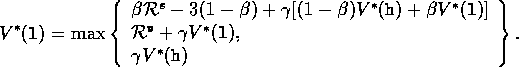
For any choice of  ,
, 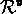 ,
, 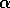 ,
, 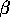 ,
and
,
and 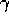 , with
, with 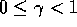 ,
, 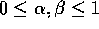 , there is exactly
one pair of numbers,
, there is exactly
one pair of numbers, 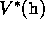 and
and 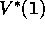 , that simultaneously satisfy these two
nonlinear equations.
, that simultaneously satisfy these two
nonlinear equations.
Example 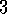 .
.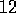
Solving the Gridworld.
Suppose we solve the Bellman equation for 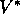 for the simple grid task
introduced in the previous example and shown again in
Figure 3.8a. Recall that state A is followed by a reward of +10
and transition to state
for the simple grid task
introduced in the previous example and shown again in
Figure 3.8a. Recall that state A is followed by a reward of +10
and transition to state 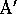 , while state B is followed by a reward of +5 and
transition to state
, while state B is followed by a reward of +5 and
transition to state 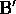 . Figure 3.8b shows the optimal
value function, and Figure 3.8c shows the corresponding optimal
policies. Where there are multiple arrows in a cell, any of the corresponding
actions is optimal.
. Figure 3.8b shows the optimal
value function, and Figure 3.8c shows the corresponding optimal
policies. Where there are multiple arrows in a cell, any of the corresponding
actions is optimal.
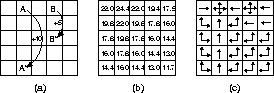
Figure:
Explicitly solving the Bellman optimality equation
provides one route for finding an optimal policy and thus to solving the reinforcement
learning problem. However, this solution is rarely directly useful. It is akin to
an exhaustive search, looking ahead at all possibilities, computing their probabilities
of occurrence, and their desirabilities in terms of expected rewards. This solution
relies on at least three assumptions that are never completely true in practice: 1)
we accurately know the dynamics of the environment, 2) we have
enough computational resources to complete the computation of the solution, and 3)
the Markov property. For the kinds of tasks in which we are interested, one is
generally not able to implement this solution exactly because various combinations
of these assumptions are violated. For example, although the first and third
assumptions present no problems for the game of backgammon, the second is a
major impediment. Since the game has about
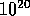 states, it would take thousands of years on today's fastest computers to
solve the Bellman equation for
states, it would take thousands of years on today's fastest computers to
solve the Bellman equation for 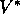 , and the same is true for
finding
, and the same is true for
finding 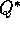 . In reinforcement learning one typically has to settle for
approximate solutions.
. In reinforcement learning one typically has to settle for
approximate solutions.
Many different decision-making methods can be viewed as
ways of approximately solving the Bellman optimality equation. For example, heuristic
search methods can be viewed as expanding the right-hand side of
(3.15) several times, up to some depth, forming a
``tree'' of possibilities, and then using a heuristic evaluation function to
approximate 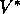 at the ``leaf'' nodes. (Heuristic search methods such as
at the ``leaf'' nodes. (Heuristic search methods such as 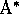 are almost always based on the total-reward case.) The methods of dynamic
programming can be related even more closely to the Bellman optimality equation. Many
reinforcement learning methods can be clearly understood as approximately solving the
Bellman optimality equation, using actual experienced transitions in place of knowledge
of the expected transitions. We consider a variety of such methods in the following
chapters.
are almost always based on the total-reward case.) The methods of dynamic
programming can be related even more closely to the Bellman optimality equation. Many
reinforcement learning methods can be clearly understood as approximately solving the
Bellman optimality equation, using actual experienced transitions in place of knowledge
of the expected transitions. We consider a variety of such methods in the following
chapters.
Exercise  .
.
Draw or describe the optimal state-value function for the golf example.
Exercise  .
.
Draw or describe the contours of the optimal action-value function for putting,
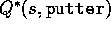 .
.
Exercise 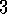 .
.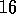
Give the Bellman equation for 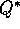 for the recycling robot.
for the recycling robot.
Exercise 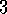 .
.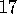
Figure 3.8 gives the optimal value of the best state of the
gridworld as 24.4, to one decimal place. Use your knowledge of the optimal policy and
(3.2) to compute this value symbolically, and then to
three decimal places.



Next: 3.9 Optimality and Approximation
Up: 3 The Reinforcement Learning
Previous: 3.7 Value Functions
Richard Sutton
Sat May 31 13:56:52 EDT 1997
 is defined to be better than or equal to a policy
is defined to be better than or equal to a policy 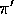 if its expected return
is greater than or equal to that of
if its expected return
is greater than or equal to that of 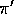 for all states. In other words,
for all states. In other words,
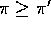 if and only if
if and only if
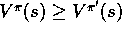 for all
for all 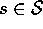 . There is always at least one
policy that is better than or equal to all other policies. This is an
optimal policy. Although there may be more than one, we denote all the optimal
policies by
. There is always at least one
policy that is better than or equal to all other policies. This is an
optimal policy. Although there may be more than one, we denote all the optimal
policies by 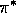 . They share the same value function, called the
optimal value function, denoted
. They share the same value function, called the
optimal value function, denoted
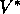 , defined as
, defined as



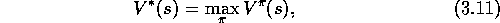
 .
.
 , defined as
, defined as
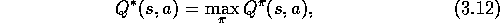
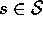 and
and 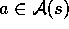 .
For state-action pair
.
For state-action pair 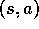 , this function gives the expected return for
taking action a in state s and thereafter following an optimal policy.
Thus, we can write
, this function gives the expected return for
taking action a in state s and thereafter following an optimal policy.
Thus, we can write 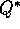 in terms of
in terms of 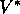 as follows:
as follows:
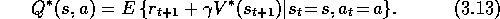
 .
. Optimal Value Functions for Golf.
The lower part of Figure
Optimal Value Functions for Golf.
The lower part of Figure 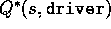 . These are the values of each
state if we first play a stroke with the driver and then afterwards select either the
driver or the putter, whichever is best. The driver enables us to hit the ball
farther, but with less accuracy. We can reach the hole in one shot using the
driver only if we are already very close; thus the -1 contour for
. These are the values of each
state if we first play a stroke with the driver and then afterwards select either the
driver or the putter, whichever is best. The driver enables us to hit the ball
farther, but with less accuracy. We can reach the hole in one shot using the
driver only if we are already very close; thus the -1 contour for 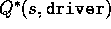 covers only a small portion of the green. If we have two strokes,
however, then we can reach the hole from much farther away, as shown by the
-2 contour. In this case we don't have to drive all the way to within the small
-1 contour, but only to anywhere on the green; from there we can use the putter.
The optimal action-value function gives the values after committing to a
particular first action, in this case, to the driver, but afterwards using
whichever actions are best. The -3 contour is still farther out and includes the
starting tee. From the tee, the best sequence of actions is two drives and one
putt, sinking the ball in three strokes.
covers only a small portion of the green. If we have two strokes,
however, then we can reach the hole from much farther away, as shown by the
-2 contour. In this case we don't have to drive all the way to within the small
-1 contour, but only to anywhere on the green; from there we can use the putter.
The optimal action-value function gives the values after committing to a
particular first action, in this case, to the driver, but afterwards using
whichever actions are best. The -3 contour is still farther out and includes the
starting tee. From the tee, the best sequence of actions is two drives and one
putt, sinking the ball in three strokes.
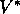 is the value function for a policy, it must satisfy the
self-consistency condition given by the Bellman equation for
state values (
is the value function for a policy, it must satisfy the
self-consistency condition given by the Bellman equation for
state values (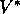 's consistency condition can be written in a special form without
reference to any specific policy. This is the Bellman equation for
's consistency condition can be written in a special form without
reference to any specific policy. This is the Bellman equation for 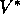 , or the
Bellman optimality equation. Intuitively,
the Bellman optimality equation expresses the fact that the value of a state under
an optimal policy must equal the expected return for the best action from that state:
, or the
Bellman optimality equation. Intuitively,
the Bellman optimality equation expresses the fact that the value of a state under
an optimal policy must equal the expected return for the best action from that state:
 .
The Bellman optimality equation for
.
The Bellman optimality equation for 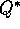 is
is
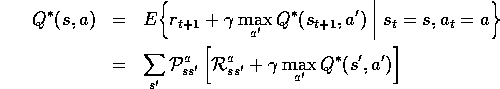
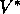 and
and
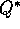 . These are the same as the backup diagrams for
. These are the same as the backup diagrams for 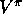 and
and 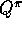 except
that arcs have been added at the agent's choice points to represent that the maximum
over that choice is taken rather than the expected value given some policy.
Figure
except
that arcs have been added at the agent's choice points to represent that the maximum
over that choice is taken rather than the expected value given some policy.
Figure 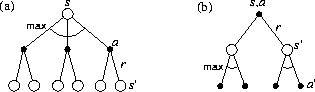
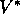 and b)
and b) 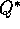
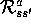 and
and 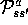 ), then
in principle one can solve this system of equations for
), then
in principle one can solve this system of equations for 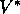 using any one of a
variety of methods for solving systems of nonlinear equations. One can solve a
related set of equations for
using any one of a
variety of methods for solving systems of nonlinear equations. One can solve a
related set of equations for
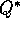 .
.
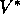 , it is relatively easy to determine an optimal policy.
For each state s, there will be one or more actions at which the maximum is obtained
in the Bellman optimality equation.
Any policy that assigns non-zero probability only to these actions is an optimal
policy. You can think of this as a one-step search. If you have the optimal value
function,
, it is relatively easy to determine an optimal policy.
For each state s, there will be one or more actions at which the maximum is obtained
in the Bellman optimality equation.
Any policy that assigns non-zero probability only to these actions is an optimal
policy. You can think of this as a one-step search. If you have the optimal value
function, 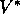 , then the actions that appear best after just a one-step search will
be optimal actions.
Another way of saying this is that any policy that is
greedy with respect to the optimal evaluation function
, then the actions that appear best after just a one-step search will
be optimal actions.
Another way of saying this is that any policy that is
greedy with respect to the optimal evaluation function 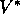 is an optimal
policy. The term greedy is used in computer science to describe any search or decision
procedure that selects alternatives based only on local or immediate considerations,
without considering the possibility that such a selection may prevent future access
to even better alternatives. Consequently, it describes policies
that select actions based only on their short-term consequences. The beauty of
is an optimal
policy. The term greedy is used in computer science to describe any search or decision
procedure that selects alternatives based only on local or immediate considerations,
without considering the possibility that such a selection may prevent future access
to even better alternatives. Consequently, it describes policies
that select actions based only on their short-term consequences. The beauty of
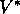 is that if one uses it to evaluate the short-term
consequences of actions, specifically, the one-step consequences, then
a greedy policy is actually optimal in the long-term sense in which we are
interested because
is that if one uses it to evaluate the short-term
consequences of actions, specifically, the one-step consequences, then
a greedy policy is actually optimal in the long-term sense in which we are
interested because 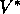 already takes into account the reward consequences of all
possible future behavior. By means of
already takes into account the reward consequences of all
possible future behavior. By means of 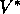 , the optimal expected long-term return is
turned into a quantity that is locally and immediately available for each state.
Hence, a one-step ahead search yields the long-term optimal actions.
, the optimal expected long-term return is
turned into a quantity that is locally and immediately available for each state.
Hence, a one-step ahead search yields the long-term optimal actions.
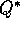 makes choosing optimal actions still
easier. With
makes choosing optimal actions still
easier. With 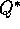 , the agent does not even have to do a one-step
ahead search: for any state s, it can simply find any action which
maximizes
, the agent does not even have to do a one-step
ahead search: for any state s, it can simply find any action which
maximizes 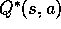 . The
action-value function effectively caches the results of all one-step ahead
searches. It provides the optimal expected long-term return as a value that is
locally and immediately available for each state-action pair. Hence, at the cost of
representing a function of state-action pairs, instead of just of states, the
optimal action value function allows optimal actions to be selected without having
to know anything about possible successor states and their values, that is, without
having to know anything about the environment's dynamics.
. The
action-value function effectively caches the results of all one-step ahead
searches. It provides the optimal expected long-term return as a value that is
locally and immediately available for each state-action pair. Hence, at the cost of
representing a function of state-action pairs, instead of just of states, the
optimal action value function allows optimal actions to be selected without having
to know anything about possible successor states and their values, that is, without
having to know anything about the environment's dynamics.
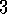 .
.
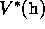 can
be written as follows:
can
be written as follows:
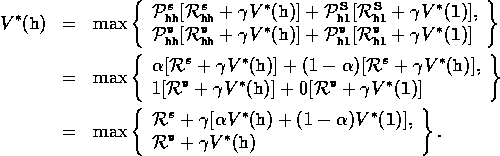
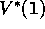 yields the equation:
yields the equation:
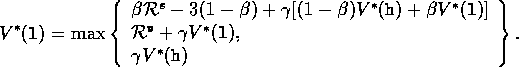
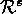 ,
, 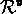 ,
, 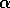 ,
, 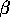 ,
and
,
and 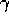 , with
, with 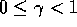 ,
, 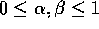 , there is exactly
one pair of numbers,
, there is exactly
one pair of numbers, 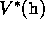 and
and 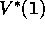 , that simultaneously satisfy these two
nonlinear equations.
, that simultaneously satisfy these two
nonlinear equations.
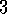 .
.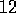
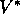 for the simple grid task
introduced in the previous example and shown again in
Figure
for the simple grid task
introduced in the previous example and shown again in
Figure 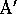 , while state B is followed by a reward of +5 and
transition to state
, while state B is followed by a reward of +5 and
transition to state 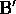 . Figure
. Figure 
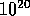 states, it would take thousands of years on today's fastest computers to
solve the Bellman equation for
states, it would take thousands of years on today's fastest computers to
solve the Bellman equation for 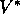 , and the same is true for
finding
, and the same is true for
finding 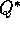 . In reinforcement learning one typically has to settle for
approximate solutions.
. In reinforcement learning one typically has to settle for
approximate solutions.
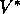 at the ``leaf'' nodes. (Heuristic search methods such as
at the ``leaf'' nodes. (Heuristic search methods such as 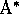 are almost always based on the total-reward case.) The methods of dynamic
programming can be related even more closely to the Bellman optimality equation. Many
reinforcement learning methods can be clearly understood as approximately solving the
Bellman optimality equation, using actual experienced transitions in place of knowledge
of the expected transitions. We consider a variety of such methods in the following
chapters.
are almost always based on the total-reward case.) The methods of dynamic
programming can be related even more closely to the Bellman optimality equation. Many
reinforcement learning methods can be clearly understood as approximately solving the
Bellman optimality equation, using actual experienced transitions in place of knowledge
of the expected transitions. We consider a variety of such methods in the following
chapters.
 .
.
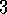 .
.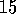
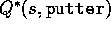 .
.
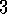 .
.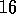
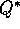 for the recycling robot.
for the recycling robot.
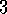 .
.