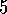Next: 3.4 A Unified Notation
Up: 3 The Reinforcement Learning
Previous: 3.2 Goals and Rewards
So far we have been imprecise regarding the objective of learning. We
have said that the agent's goal is to maximize the reward it receives in the long
run. How might this be formally defined? If the sequence of rewards received after
time step
t is denoted 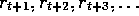 , then what precise aspect of this
sequence do we wish to maximize? In general, we seek to maximize the expected
return, where the return,
, then what precise aspect of this
sequence do we wish to maximize? In general, we seek to maximize the expected
return, where the return, 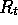 , is defined as some specific function of the reward
sequence. In the simplest case the return is just the sum of the rewards:
, is defined as some specific function of the reward
sequence. In the simplest case the return is just the sum of the rewards:

where T is a final time step. This approach makes sense in applications in
which there is a natural notion of final time step, that is, when the
agent-environment interaction breaks naturally into subsequences, which we call
episodes, such as plays of a game, trips
through a maze, or any sort of repeated interactions. Each episode ends in a
special state called the terminal state, followed by a reset to a
standard starting state or to a standard distribution of starting states.
Tasks with episodes of this kind are called episodic tasks. In
episodic tasks we sometimes need to distinguish the set of all non-terminal
states, denoted
such as plays of a game, trips
through a maze, or any sort of repeated interactions. Each episode ends in a
special state called the terminal state, followed by a reset to a
standard starting state or to a standard distribution of starting states.
Tasks with episodes of this kind are called episodic tasks. In
episodic tasks we sometimes need to distinguish the set of all non-terminal
states, denoted 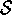 , and the set of all states plus the terminal state,
denoted
, and the set of all states plus the terminal state,
denoted 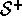 .
.
On the other hand, in many cases that the agent-environment interaction
does not break naturally into identifiable episodes, but simply goes on and on
without limit. For example, this would be the natural way to formulate a
continual process-control task, or an application to a robot with a long
lifespan. We call these continual tasks.
The return formulation (3.1) is problematic for continual tasks
because the final time step would be 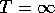 , and the return, which is what we are
trying to maximize, could itself easily be infinite. (For example, suppose the agent
receives a reward of +1 at each time step.) Thus, in this book we use a
definition of return that is slightly more complex conceptually but much simpler
mathematically.
, and the return, which is what we are
trying to maximize, could itself easily be infinite. (For example, suppose the agent
receives a reward of +1 at each time step.) Thus, in this book we use a
definition of return that is slightly more complex conceptually but much simpler
mathematically.
The additional concept that we need is that of discounting.
According to this approach, the agent tries to select actions so that the
sum of the discounted rewards it receives over the future is maximized. In
particular, it chooses  to maximize the expected discounted
return:
to maximize the expected discounted
return:
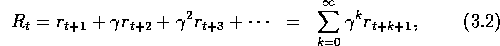
where 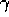 is a parameter,
is a parameter, 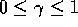 , called the discount rate.
, called the discount rate.
The discount rate determines the present value of future rewards:
a reward received k time steps in the future is worth only 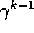 times
what it would be worth if it were received immediately. If
times
what it would be worth if it were received immediately. If 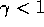 , the infinite
sum has a finite value as long as the reward sequence
, the infinite
sum has a finite value as long as the reward sequence 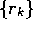 is bounded. If
is bounded. If
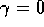 , the agent is ``myopic" in being only concerned with maximizing immediate
rewards: its objective in this case is to learn how to choose
, the agent is ``myopic" in being only concerned with maximizing immediate
rewards: its objective in this case is to learn how to choose 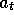 so as maximize
only
so as maximize
only 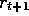 . If each of the agent's actions happened only to influence the
immediate reward, not future rewards as well, then a myopic agent could maximize
(3.2) by separately maximizing each immediate reward. But in
general, acting to maximize immediate reward can reduce access to future rewards so
that the return may actually be reduced. As
. If each of the agent's actions happened only to influence the
immediate reward, not future rewards as well, then a myopic agent could maximize
(3.2) by separately maximizing each immediate reward. But in
general, acting to maximize immediate reward can reduce access to future rewards so
that the return may actually be reduced. As 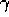 approaches one, the objective
takes future rewards into account more strongly: the agent becomes more far-sighted.
approaches one, the objective
takes future rewards into account more strongly: the agent becomes more far-sighted.
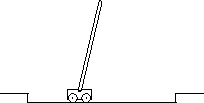
Figure 3.2: The pole-balancing task
Example 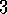 .
.
Pole Balancing.
Figure 3.2 shows a task that served as an early illustration of
reinforcement learning. The objective
here is to apply forces to a cart moving along a track so as to keep a pole hinged to
the cart from falling over. A failure is said to occur if the pole falls
past a given angle from vertical or if the cart exceeds the limits of the track. The
pole is reset to vertical after each failure. This task could be treated
as episodic, where the natural episodes are the repeated
attempts to balance the pole. The reward in this case could be +1 for every time
step on which failure did not occur, so that the return at each time would be the
number of steps until failure. Alternatively, we could treat pole balancing as a
continual task, using discounting. In this case the reward would be -1 on
each failure and zero at all other times. The return at each time would then
be related to 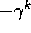 , where k is the number of time steps before failure. In
either case, the return is maximized by keeping the pole balanced for as long as
possible.
, where k is the number of time steps before failure. In
either case, the return is maximized by keeping the pole balanced for as long as
possible.
Exercise  .
.
Suppose you treated pole-balancing as an episodic task but also used
discounting, with all rewards zero except for a -1 upon failure. What then would
the return be at each time? How does this return differ from that in the
discounted, continual formulation of this task?
Exercise  .
.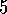
Imagine that you are designing a robot to run a maze. You decide to give it a
reward of +1 for escaping from the maze and a reward of zero at all other
times. The task seems to break down naturally into episodes---the successive
runs through the maze---so you decide to treat it as an episodic task, where
the goal is to maximize expected total reward (3.1).
After running the learning
agent for a while, you find that it is showing no improvement in escaping from the
maze. What is going wrong? Have you effectively communicated to the
agent what you want it to achieve?



Next: 3.4 A Unified Notation
Up: 3 The Reinforcement Learning
Previous: 3.2 Goals and Rewards
Richard Sutton
Sat May 31 13:56:52 EDT 1997
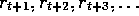 , then what precise aspect of this
sequence do we wish to maximize? In general, we seek to maximize the expected
return, where the return,
, then what precise aspect of this
sequence do we wish to maximize? In general, we seek to maximize the expected
return, where the return, 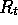 , is defined as some specific function of the reward
sequence. In the simplest case the return is just the sum of the rewards:
, is defined as some specific function of the reward
sequence. In the simplest case the return is just the sum of the rewards:





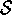 , and the set of all states plus the terminal state,
denoted
, and the set of all states plus the terminal state,
denoted 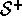 .
.
 , and the return, which is what we are
trying to maximize, could itself easily be infinite. (For example, suppose the agent
receives a reward of +1 at each time step.) Thus, in this book we use a
definition of return that is slightly more complex conceptually but much simpler
mathematically.
, and the return, which is what we are
trying to maximize, could itself easily be infinite. (For example, suppose the agent
receives a reward of +1 at each time step.) Thus, in this book we use a
definition of return that is slightly more complex conceptually but much simpler
mathematically.
 to maximize the expected discounted
return:
to maximize the expected discounted
return:
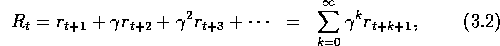
 is a parameter,
is a parameter, 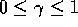 , called the discount rate.
, called the discount rate.
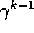 times
what it would be worth if it were received immediately. If
times
what it would be worth if it were received immediately. If 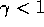 , the infinite
sum has a finite value as long as the reward sequence
, the infinite
sum has a finite value as long as the reward sequence 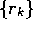 is bounded. If
is bounded. If
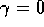 , the agent is ``myopic" in being only concerned with maximizing immediate
rewards: its objective in this case is to learn how to choose
, the agent is ``myopic" in being only concerned with maximizing immediate
rewards: its objective in this case is to learn how to choose 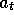 so as maximize
only
so as maximize
only 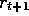 . If each of the agent's actions happened only to influence the
immediate reward, not future rewards as well, then a myopic agent could maximize
(
. If each of the agent's actions happened only to influence the
immediate reward, not future rewards as well, then a myopic agent could maximize
(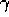 approaches one, the objective
takes future rewards into account more strongly: the agent becomes more far-sighted.
approaches one, the objective
takes future rewards into account more strongly: the agent becomes more far-sighted.

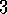 .
.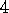
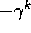 , where k is the number of time steps before failure. In
either case, the return is maximized by keeping the pole balanced for as long as
possible.
, where k is the number of time steps before failure. In
either case, the return is maximized by keeping the pole balanced for as long as
possible.
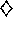
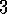 .
.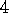
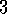 .
.