


Next: 3.5 The Markov Property
Up: 3 The Reinforcement Learning
Previous: 3.3 Returns
In the preceding section we described two kinds of reinforcement learning tasks,
one in which the agent-environment interaction naturally breaks down into a
sequence of separate episodes (episodic tasks), and one in which it does not
(continual tasks). The former case is mathematically easier because each
action affects only the finite number of rewards subsequently received during the
episode.
In this book we consider sometimes one kind of problem and sometimes the other,
but often both. It is therefore useful to establish one
notation that enables us to talk precisely about both cases simultaneously.
To be precise about episodic tasks requires some additional notation.
Rather than one long sequence of time steps, we need to consider a series of
episodes, each of which consists of a finite sequence of time steps.
We number the time steps of each episode starting anew from zero.
Therefore, we have to refer
not just to 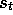 , the state representation at time t, but to
, the state representation at time t, but to 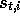 , the
state representation at time
t of episode i (and similarly for
, the
state representation at time
t of episode i (and similarly for 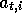 ,
, 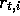 ,
, 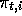 ,
, 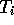 , etc.).
However, it turns out that when we discuss episodic tasks we will almost never
have to distinguish between different episodes. We will almost always be
considering a particular single episode, or stating something that is true for
all episodes. Accordingly, in practice we will almost always abuse notation
slightly by dropping the explicit reference to episode number. That is, we
will simply write
, etc.).
However, it turns out that when we discuss episodic tasks we will almost never
have to distinguish between different episodes. We will almost always be
considering a particular single episode, or stating something that is true for
all episodes. Accordingly, in practice we will almost always abuse notation
slightly by dropping the explicit reference to episode number. That is, we
will simply write 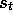 to refer to
to refer to 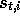 , etc.
, etc.
We need one other convention to obtain a single notation that covers
both episodic and continual tasks. We have defined the return
as a sum over a finite number of terms in one case (3.1) and as a
sum over an infinite number of terms in the other (3.2). These can be
unified by considering episode termination to be the entering of a special
absorbing state that transitions only to itself and which generates only
rewards of zero. For example, consider the state transition diagram:
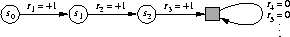
Here the solid square represents the special absorbing state corresponding to
the end of an episode. Starting from 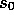 we get the reward sequence
we get the reward sequence
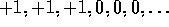 . Summing these up, we get the same return whether we sum
over the first T rewards (here T=3) or we sum over the full infinite
sequence. This remains true even if we introduce discounting. Thus, we can
define the return, in general, as
. Summing these up, we get the same return whether we sum
over the first T rewards (here T=3) or we sum over the full infinite
sequence. This remains true even if we introduce discounting. Thus, we can
define the return, in general, as
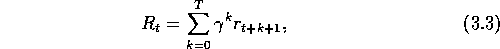
including the possibility that either 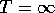 or
or 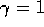 (but not
both
(but not
both ), and using the convention of
omitting episode numbers when they are not needed. We use these conventions
throughout the rest of the book to simplify notation and to express the close
parallels between episodic and continual tasks.
), and using the convention of
omitting episode numbers when they are not needed. We use these conventions
throughout the rest of the book to simplify notation and to express the close
parallels between episodic and continual tasks.



Next: 3.5 The Markov Property
Up: 3 The Reinforcement Learning
Previous: 3.3 Returns
Richard Sutton
Sat May 31 13:56:52 EDT 1997
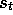 , the state representation at time t, but to
, the state representation at time t, but to 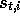 , the
state representation at time
t of episode i (and similarly for
, the
state representation at time
t of episode i (and similarly for 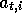 ,
, 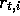 ,
, 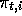 ,
, 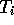 , etc.).
However, it turns out that when we discuss episodic tasks we will almost never
have to distinguish between different episodes. We will almost always be
considering a particular single episode, or stating something that is true for
all episodes. Accordingly, in practice we will almost always abuse notation
slightly by dropping the explicit reference to episode number. That is, we
will simply write
, etc.).
However, it turns out that when we discuss episodic tasks we will almost never
have to distinguish between different episodes. We will almost always be
considering a particular single episode, or stating something that is true for
all episodes. Accordingly, in practice we will almost always abuse notation
slightly by dropping the explicit reference to episode number. That is, we
will simply write 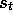 to refer to
to refer to 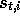 , etc.
, etc.



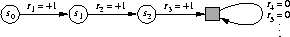
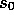 we get the reward sequence
we get the reward sequence
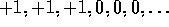 . Summing these up, we get the same return whether we sum
over the first T rewards (here T=3) or we sum over the full infinite
sequence. This remains true even if we introduce discounting. Thus, we can
define the return, in general, as
. Summing these up, we get the same return whether we sum
over the first T rewards (here T=3) or we sum over the full infinite
sequence. This remains true even if we introduce discounting. Thus, we can
define the return, in general, as
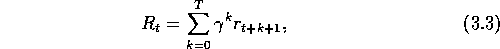
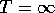 or
or 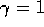 (but not
both
(but not
both