The n -armed bandit problem we considered above is a case in which the feedback is purely evaluative. The reward received after each action gives some information about how good the action was, but it says nothing at all about whether the action was correct or incorrect, that is, whether it was a best action or not. Here, correctness is a relative property of actions that can only be determined by trying them all and comparing their rewards. In this sense the problem is inherently one requiring explicit search among the alternative actions. You have to perform some form of the generate-and-test method whereby you try actions, observe the outcomes, and selectively retain those that are the most effective. This is learning by selection, in contrast to learning by instruction, and all reinforcement learning methods have to use it in one form or another.
This contrasts sharply with supervised-learning, where the feedback from the environment directly indicates what the correct action should have been. In this case there is no need to search: whatever action you try, you will be told what the right one would have been. There is no need to try a variety of actions; the instructive ``feedback" is typically independent of the action selected (so is not really feedback at all). It might still be necessary to search in the parameter space of the supervised learning system (e.g., the weight-space of a neural network), but searching in the space of actions is not required.
Of course, supervised learning is usually applied to problems that are much more complex in some ways than the n -armed bandit. In supervised learning there is not one situation in which action is taken, but a large set of different situations, each of which must be responded to correctly. The main problem facing a supervised learning system is to construct a mapping from the situations to actions that mimics the correct actions specified by the environment and that generalizes correctly to new situations. A supervised learning system cannot be said to learn to control its environment because it follows, rather than influences, the instructive information it receives. Instead of trying to make its environment behave in a certain way, it tries to make itself behave as instructed by its environment.
Focusing on the special case of a single situation that is
encountered repeatedly helps make plain the distinction between
evaluation and instruction. Suppose there
are 100 possible actions and you select action number 32. Evaluative
feedback would give you a score, say 0.9, for that action whereas
instructive training information would say what other action, say action
number 67, would actually have been correct. The latter is clearly much
more informative training information. Even if instructional information
is noisy, it is still more informative than evaluative feedback. It is
always true that a single instruction can be used to advantage to
direct changes in the action selection rule, whereas evaluative feedback
must be compared with that of other actions before any inferences can be
made about action selection.
The difference between evaluative feedback and instructive information remains significant even if there are only two actions and two possible rewards. For these binary bandit tasks, let us call the two rewards success and failure. If you received success, then you might reasonably infer that whatever action you selected was correct, and if you received failure, then you might infer that whatever action you did not select was correct. You could then keep a tally of how often each action was (inferred to be) correct and select the action that was correct most often. Let us call this the supervised algorithm because it corresponds most closely to what supervised learning methods might do in the case of only a single input pattern. If the rewards are deterministic, then the inferences of the supervised algorithm are all correct and it performs excellently. If the rewards are stochastic, then the picture is more complicated.
In the stochastic case, a particular binary bandit task is defined by two numbers, the probabilities of success for each possible action. The space of all possible tasks is thus a unit square, as shown in Figure 2.2. The upper-left and lower-right quadrants correspond to relatively easy tasks for which the supervised algorithm would work well. For these, the probability of success for the better action is greater than a half and the probability of success for the poorer action is less than a half. For these tasks, the action inferred to be correct as described above will actually be the correct action more than half the time.
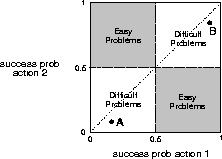
Figure 2.2: The easy and difficult regions in the space of all binary bandit tasks.
However, binary bandit tasks in the other two quadrants of Figure 2.2 are more difficult and cannot be solved effectively by the supervised algorithm. For example, consider a task with success probabilities .1 and .2, corresponding to point A in the lower-left difficult quadrant of Figure 2.2. Because both actions produce failure at least 80% of the time, any method that takes failure as an indication that the other action was correct will oscillate between the two actions, never settling on the better one. Now consider a task with success probabilities .8 and .9, corresponding to point B in the upper-right difficult quadrant of Figure 2.2. In this case both actions produce success almost all the time. Any method that takes success as an indication of correctness can easily become stuck selecting the wrong action.
Figure 2.3 shows the average behavior of the supervised
algorithm and several other algorithms on the binary bandit tasks corresponding to
points A and B. For comparison, also shown is the behavior of an 
-greedy
action-value method (
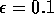) as described in Section 2.2. In both
tasks, the supervised algorithm learns to select the better action only slightly more
than half the time.
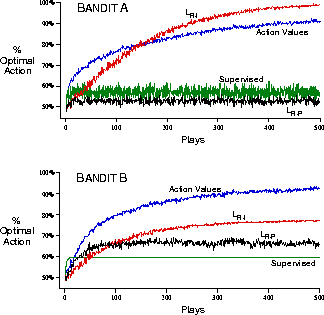
Figure 2.3: Performance of selected algorithms on the binary bandit tasks corresponding
to points A and B in Figure 2.2. These data are averages over
2000 runs.
The graphs in Figure 2.3 also show the average
behavior of two other algorithms, known as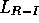 
and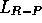 
. These are
classical methods from the field of learning automata that follow
a logic similar to that of the supervised algorithm. Both methods are
stochastic, updating the probabilities of selecting each action, denoted
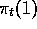and 
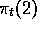. The
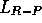method infers the correct action just as the supervised algorithm does, and then
adjusts its probabilities as follows. If the action inferred to be
correct on play t was
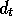, then
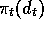is incremented a fraction, 
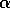, of the
way from its current value towards one:
The probability of the other action is adjusted inversely, so that the two
probabilities sum to one. For the results shown in
Figure 2.3,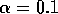 
. The idea of 
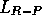is very similar to
that of the supervised algorithm, only it is stochastic. Rather than committing
totally to the action inferred to be best,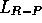 
gradually increases its
probability.
The name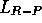 
stands for ``linear, reward-penalty," meaning that the update
(2.3) is linear in the probabilities and that the update is
performed on both success (reward) plays and failure (penalty) plays. The name
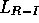stands for ``linear, reward-inaction." This algorithm is identical to
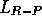except that it only updates its probabilities upon success plays; failure
plays are ignored entirely. The results in Figure 2.3 show
that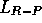 
performs little, if any, better than the supervised algorithm on the
binary bandit tasks corresponding to points A and B in
Figure 2.2. 
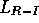eventually performs very well on the A
task, but not on the B task, and learns slowly in both cases.
Binary bandit problems are an instructive special case blending aspects of supervised and reinforcement learning problems. Because the rewards are binary, it is possible to infer something about the correct action given just a single reward. On some instances of such problems, these inferences are quite reasonable and lead to effective algorithms. In other instances, however, such inferences are less appropriate and lead to poor behavior. In bandit problems with non-binary rewards, such as the 10-armed test bandit introduced in Section 2.2, it is not at all clear how the ideas behind these inferences could be applied to produce effective algorithms. All of these are very simple problems, but already we see the need for capabilities beyond those of supervised learning methods.
Exercise 
.
Consider a simplified supervised learning problem in which there is only one situation (input pattern) and two actions. One action, say a, is correct and the other, b, is incorrect. The instruction signal is noisy: it instructs the wrong action with probability p; that is, with probability p it says that b is correct. You can think of this as a binary bandit problem if you treat agreeing with the (possibly wrong) instruction signal as success, and disagreeing with it as failure. Discuss the resulting class of binary bandit problems. Is anything special about these problems? How does the supervised algorithm perform on this type of problem?
