First we consider how to compute the state-value function ![]() for an
arbitrary policy
for an
arbitrary policy ![]() . This is called policy evaluation in the DP
literature. We also refer to it as the prediction problem. Recall from
Chapter 3 that, for all
. This is called policy evaluation in the DP
literature. We also refer to it as the prediction problem. Recall from
Chapter 3 that, for all
![]() ,
,
If the environment's dynamics are
completely known, then (4.4) is a system of ![]() simultaneous
linear equations in
simultaneous
linear equations in
![]() unknowns (the
unknowns (the ![]() ,
, ![]() ). In principle, its solution is a
straightforward, if tedious, computation. For our purposes, iterative solution
methods are most suitable. Consider a sequence of approximate value functions
). In principle, its solution is a
straightforward, if tedious, computation. For our purposes, iterative solution
methods are most suitable. Consider a sequence of approximate value functions
![]() , each mapping
, each mapping ![]() to
to ![]() . The initial
approximation,
. The initial
approximation,
![]() , is chosen arbitrarily (except that the terminal state, if any, must be
given value 0), and each successive approximation is obtained by using the
Bellman equation for
, is chosen arbitrarily (except that the terminal state, if any, must be
given value 0), and each successive approximation is obtained by using the
Bellman equation for ![]() (3.10) as an update rule:
(3.10) as an update rule:
To produce each successive approximation, ![]() from
from ![]() , iterative policy
evaluation applies the same operation to each state
, iterative policy
evaluation applies the same operation to each state ![]() : it replaces the old value
of
: it replaces the old value
of ![]() with a new value obtained from the old values of the successor states of
with a new value obtained from the old values of the successor states of
![]() , and the expected immediate rewards, along all the one-step transitions
possible under the policy being evaluated. We call this kind of operation a full backup. Each iteration of iterative policy evaluation backs
up the value of every state once to produce the new approximate value function
, and the expected immediate rewards, along all the one-step transitions
possible under the policy being evaluated. We call this kind of operation a full backup. Each iteration of iterative policy evaluation backs
up the value of every state once to produce the new approximate value function
![]() . There are several different kinds of full backups, depending on whether
a state (as here) or a state-action pair is being backed up, and depending on the
precise way the estimated values of the successor states are combined. All the
backups done in DP algorithms are called full backups because they are
based on all possible next states rather than on a sample next state. The nature
of a backup can be expressed in an equation, as above, or in a backup diagram like
those introduced in Chapter 3. For example, Figure 3.4a is the
backup diagram corresponding to the full backup used in iterative policy
evaluation.
. There are several different kinds of full backups, depending on whether
a state (as here) or a state-action pair is being backed up, and depending on the
precise way the estimated values of the successor states are combined. All the
backups done in DP algorithms are called full backups because they are
based on all possible next states rather than on a sample next state. The nature
of a backup can be expressed in an equation, as above, or in a backup diagram like
those introduced in Chapter 3. For example, Figure 3.4a is the
backup diagram corresponding to the full backup used in iterative policy
evaluation.
To write a sequential computer program to implement iterative policy evaluation, as
given by (4.5), you would have to use two arrays, one for
the old values, ![]() , and one for the new values,
, and one for the new values, ![]() . This way, the
new values can be computed one by one from the old values without the
old values being changed. Of course it is easier to use one array and
update the values "in place," that is, with each new backed-up value immediately
overwriting the old one. Then, depending on the order in which the states
are backed up, sometimes new values are used instead of old ones on the
right-hand side of (4.5). This slightly different algorithm also
converges to
. This way, the
new values can be computed one by one from the old values without the
old values being changed. Of course it is easier to use one array and
update the values "in place," that is, with each new backed-up value immediately
overwriting the old one. Then, depending on the order in which the states
are backed up, sometimes new values are used instead of old ones on the
right-hand side of (4.5). This slightly different algorithm also
converges to ![]() ; in fact, it usually converges faster than the two-array
version, as you might expect, since it uses new data as soon as they are available.
We think of the backups as being done in a sweep through the state space.
For the in-place algorithm, the order in which states are backed up during the
sweep has a significant influence on the rate of convergence. We usually have the
in-place version in mind when we think of DP algorithms.
; in fact, it usually converges faster than the two-array
version, as you might expect, since it uses new data as soon as they are available.
We think of the backups as being done in a sweep through the state space.
For the in-place algorithm, the order in which states are backed up during the
sweep has a significant influence on the rate of convergence. We usually have the
in-place version in mind when we think of DP algorithms.
Another implementation point concerns the termination of the algorithm.
Formally, iterative policy evaluation converges only in the limit, but in practice
it must be halted short of this. A typical stopping condition for
iterative policy evaluation is to test the quantity ![]() after each sweep and stop when it is sufficiently small.
Figure
4.1 gives a complete algorithm for
iterative policy evaluation with this stopping criterion.
after each sweep and stop when it is sufficiently small.
Figure
4.1 gives a complete algorithm for
iterative policy evaluation with this stopping criterion.
Example 4.1 Consider the
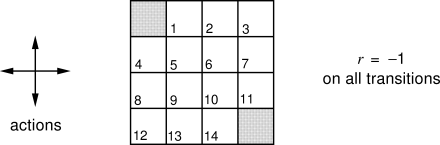
|

Exercise 4.1 If
Exercise 4.2 Suppose a new state 15 is added to the gridworld just below state 13, and its actions, left, up, right, and down, take the agent to states 12, 13, 14, and 15, respectively. Assume that the transitions from the original states are unchanged. What, then, is
Exercise 4.3 What are the equations analogous to (4.3), (4.4), and (4.5) for the action-value function
Exercise 4.3.5 In some undiscounted episodic tasks there may be policies for which eventual termination is not guaranteed. For example, in the grid problem above it is possible to go back and forth between two states forever. In a task that is otherwise perfectly sensible,