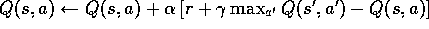Next: 9.2 Integrating PlanningActing,
Up: 9 Planning and Learning
Previous: 9 Planning and Learning
By a model of the environment we mean anything that an agent can use to
predict how the environment will respond to its actions. Given a state and
an action, a model produces a prediction of the resultant next
state and next reward. If the model is stochastic, then there are several
possible next states and next rewards, each with some probability of occurring.
Some models produce a description of all possibilities and their
probabilities; these we call distribution models. Other models produce
just one of the possibilities, sampled according to the probabilities; these we
call sample models. For example, consider modeling the sum of a dozen dice.
A distribution model would produce all possible sums and their probabilities of
occurring, whereas a sample model would produce an individual sum drawn according
to this probability distribution. The kind of model assumed in dynamic
programming---estimates of the state transition probabilities and expected rewards,
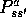 and
and
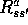 ---is a distribution model. The kind of model used in the blackjack
example in Chapter 5 is a sample model. Distribution models are stronger than
sample models in that they can always be used to produce samples. However, in
surprisingly many applications it is much easier to obtain sample models than
distribution models.
---is a distribution model. The kind of model used in the blackjack
example in Chapter 5 is a sample model. Distribution models are stronger than
sample models in that they can always be used to produce samples. However, in
surprisingly many applications it is much easier to obtain sample models than
distribution models.
Models can be used to mimic or simulate experience. Given
a starting state and action, a sample model produces a possible transition, and
a distribution model generates all possible transitions weighted by their
probabilities of occurring. Given a starting state and a policy, a sample
model could produce an entire episode, and a distribution model could generate all
possible episodes and their probabilities. In either case, we say the model is
used to simulate the environment and produce simulated experience.
The word ``planning" is used in several different ways in different fields. We use
the term to refer to any computational process that takes a model as input and
produces or improves a policy for interacting with the modeled environment:

Within artificial intelligence, there are two distinct approaches to planning
according to our definition. In state-space planning, which includes the
approach we take in this book, planning is viewed primarily as a search
through the state space for an optimal policy or path to a goal. Actions cause
transitions from state to state, and value functions are computed over states. In
what we call plan-space planning, planning is instead viewed as a search
through the space of plans. Operators transform one complete plan into another,
and value functions, if any, are defined over the space of complete plans.
Plan-space planning includes evolutionary methods and partial-order planning,
a popular kind of planning in artificial intelligence in which the ordering of
steps is not completely determined at all stages of planning. Plan-space methods
are difficult to apply efficiently to the stochastic optimal control problems that
are the focus in reinforcement learning, and we do not consider them further (but
see Section 11 .6
for one application of reinforcement learning within
plan-space planning).
The unified view we present in this chapter is that all state-space planning methods
share a common structure, a structure that is also present in the learning
methods presented in this book. It takes the rest of the chapter to
develop this view, but there are two basic ideas: 1) all state-space planning
methods involve computing value functions as a key intermediate step toward
improving the policy, and 2) they compute their value functions by backup
operations applied to simulated experience. This common structure can be
diagrammed as follows:

Dynamic programming methods clearly fit this structure: they
make sweeps through the space of states, generating for each the
distribution of possible transitions. Each distribution is then used to compute a
backed-up value and update the state's estimated value. In this chapter we argue
that a variety of other state-space planning methods also fit this structure, with
individual methods differing only in the kinds of backups they do and the order in
which they do them.
Viewing planning methods in this way emphasizes their relationship to the learning
methods that we have described in this book. The heart of both learning and
planning methods is the estimation of value functions by backup operations. The
difference is that whereas planning uses simulated experience generated
by a model, learning methods use real experience generated by the
environment. Of course this difference leads to a number of other differences, for
example, in how performance is assessed and in how flexibly experience can be
generated. But the common structure means that many ideas and algorithms can be
transferred between planning and learning. In particular, in many cases, a learning
algorithm can be substituted for the key backup step of a planning method.
Learning methods require only experience as input, and in many cases they can be
applied to simulated experience just as well as to real experience.
Figure 9.1 shows a simple example of a planning method based on
1-step tabular Q-learning and on random samples from a sample model. This
method, which we call random-sample 1-step tabular Q-planning, converges to
the optimal policy for the model under the same conditions that 1-step tabular
Q-learning converges to the optimal policy for the real environment (each
state-action pair must be selected an infinite number of times in Step 1, and 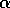 \
must decrease appropriately over time).
\
must decrease appropriately over time).
Do Forever:
1. Select a state, 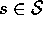 , and an action,
, and an action, 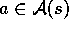 , at random
2. Send s,a to a sample model, and obtain
a sample next state,
, at random
2. Send s,a to a sample model, and obtain
a sample next state, 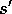 , and a sample next reward, r
3. Apply 1-step tabular Q-learning to
, and a sample next reward, r
3. Apply 1-step tabular Q-learning to 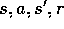 :
:
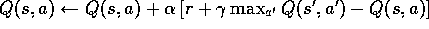
Figure 9.1: Random-sample 1-step tabular Q-planning
In addition to the unified view of planning and learning
methods, a second theme in this chapter is the benefits of planning in
small, incremental steps. This enables planning to be interrupted or
re-directed at any time with little wasted computation, which appears to be a
key requirement for efficiently intermixing planning with acting and with learning
of the model. More surprisingly, later in this chapter we present evidence that
planning in very small steps may be the most efficient approach even on pure
planning problems if the problem is too large to be solved exactly.



Next: 9.2 Integrating PlanningActing,
Up: 9 Planning and Learning
Previous: 9 Planning and Learning
Richard Sutton
Fri May 30 17:11:38 EDT 1997
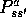 and
and
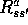 ---is a distribution model. The kind of model used in the blackjack
example in Chapter 5 is a sample model. Distribution models are stronger than
sample models in that they can always be used to produce samples. However, in
surprisingly many applications it is much easier to obtain sample models than
distribution models.
---is a distribution model. The kind of model used in the blackjack
example in Chapter 5 is a sample model. Distribution models are stronger than
sample models in that they can always be used to produce samples. However, in
surprisingly many applications it is much easier to obtain sample models than
distribution models.





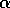 \
must decrease appropriately over time).
\
must decrease appropriately over time).
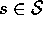 , and an action,
, and an action, 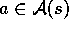 , at random
2. Send s,a to a sample model, and obtain
a sample next state,
, at random
2. Send s,a to a sample model, and obtain
a sample next state, 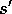 , and a sample next reward, r
3. Apply 1-step tabular Q-learning to
, and a sample next reward, r
3. Apply 1-step tabular Q-learning to 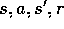 :
: