


Next: 6.4 Sarsa: On-Policy TD
Up: 6 Temporal Difference Learning
Previous: 6.2 Advantages of TD
Suppose there is available only a finite amount of experience, say 10 episodes
or 100 time steps. In this
case, a common approach with incremental learning methods is to repeatedly present
the experience until the method converges
upon an answer. Given an approximate value function, V, the increments specified
by (6.1) or (6.2) are computed for every time step t at which a
nonterminal state is visited, but the value function is only changed once, by the
sum of all the increments. Then all the available experience is processed again
with the new value function to produce a new overall increment, and so on, until the
value function converges. We call this batch updating because
updates are made only after processing each complete batch of training data.
Under batch updating, TD(0)
converges deterministically to a single answer independent of the
step-size parameter, 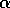 , as long as
, as long as 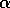 is chosen to be sufficiently small.
The constant-
is chosen to be sufficiently small.
The constant-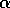 MC method also converges deterministically under the same
conditions, but to a different answer.
Understanding these two answers will help us understand the difference between
the two methods. Under normal updating the methods do not move all the way to
their respective batch answers, but in some sense they take a step in these
directions. Before trying to understand the two answers in general, for all
possible tasks, we first look at a few examples.
MC method also converges deterministically under the same
conditions, but to a different answer.
Understanding these two answers will help us understand the difference between
the two methods. Under normal updating the methods do not move all the way to
their respective batch answers, but in some sense they take a step in these
directions. Before trying to understand the two answers in general, for all
possible tasks, we first look at a few examples.
Example  .
.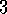 Random walk under batch updating.
Batch-updating versions of TD(0) and constant-
Random walk under batch updating.
Batch-updating versions of TD(0) and constant-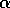 MC were applied as follows
to the random-walk prediction example (Example 6
.2). After each new
episode, all episodes seen so far were treated as a batch. They were
repeatedly presented to the algorithm, either TD(0) or constant-
MC were applied as follows
to the random-walk prediction example (Example 6
.2). After each new
episode, all episodes seen so far were treated as a batch. They were
repeatedly presented to the algorithm, either TD(0) or constant-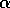 MC, with
MC, with 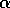 \
sufficiently small that the value function converged.
The resulting value function was then compared to
\
sufficiently small that the value function converged.
The resulting value function was then compared to 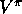 , and the
average mean-squared error across the five states (and across 100 independent
repetitions of the whole experiment) was plotted to obtain the learning curves
shown in Figure 6.8. Note that the batch TD method was
consistently better than the batch MC method.
, and the
average mean-squared error across the five states (and across 100 independent
repetitions of the whole experiment) was plotted to obtain the learning curves
shown in Figure 6.8. Note that the batch TD method was
consistently better than the batch MC method. 
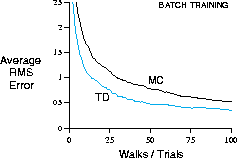
Figure 6.8: Performance of TD(0) and constant-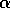 MC under batch training on the
random-walk task.
MC under batch training on the
random-walk task.
Under batch training, the MC method converges to values, 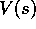 , that are the
sample averages of the actual returns experienced after visiting each state
s. These are optimal estimates in the sense that they minimize the mean-squared
error from the actual returns in the training set. In this sense it is surprising
that the batch TD method was able to perform better in the mean-squared error measure
shown in Figure 6.8. How is it that batch TD was able to perform
better than this optimal method? The answer is that MC is only optimal in a limited
way, and that TD is optimal in a way that is more relevant to predicting returns. But
first let's develop our intuitions about different kinds of optimality through
another example.
, that are the
sample averages of the actual returns experienced after visiting each state
s. These are optimal estimates in the sense that they minimize the mean-squared
error from the actual returns in the training set. In this sense it is surprising
that the batch TD method was able to perform better in the mean-squared error measure
shown in Figure 6.8. How is it that batch TD was able to perform
better than this optimal method? The answer is that MC is only optimal in a limited
way, and that TD is optimal in a way that is more relevant to predicting returns. But
first let's develop our intuitions about different kinds of optimality through
another example.
Example 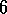 .
.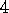 You are the Predictor.
Place yourself now in the role of the predictor of returns for a Markov
chain. Suppose you observe the following eight episodes:
You are the Predictor.
Place yourself now in the role of the predictor of returns for a Markov
chain. Suppose you observe the following eight episodes:
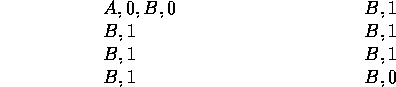
This means that the first episode started in state A, transitioned to B with a
reward of 0, and then terminated from B with a reward of 0. The other seven
episodes were even shorter, starting from B and terminating immediately. Given this
batch of data, what would you say are the optimal predictions, the best values for
the estimates
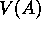 and
and 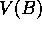 ? Everyone would probably agree that the optimal value for
? Everyone would probably agree that the optimal value for
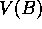 is
is 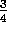 , because six out of the eight times in state
B the process terminated immediately with a return of 1, and the other two times
in B the process terminated immediately with a return of 0.
, because six out of the eight times in state
B the process terminated immediately with a return of 1, and the other two times
in B the process terminated immediately with a return of 0.
But what is the optimal value for the estimate 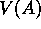 given this data? Here there are
two reasonable answers. One is to observe that 100% of the times the process was in
state A it traversed immediately to B (with a reward of 0), and we
have already decided that B has value
given this data? Here there are
two reasonable answers. One is to observe that 100% of the times the process was in
state A it traversed immediately to B (with a reward of 0), and we
have already decided that B has value 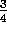 , so therefore A must have value
, so therefore A must have value
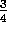 as well. One way of viewing this answer is that it is based on first
modeling the Markov process, in this case as
as well. One way of viewing this answer is that it is based on first
modeling the Markov process, in this case as
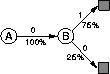
and then computing the correct estimates given the model, which indeed in this
case gives 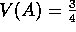 . This is also the answer that batch TD(0) gives.
. This is also the answer that batch TD(0) gives.
The
other reasonable answer is simply to observe that we have seen A once and the
return that followed it was 0, and therefore estimate 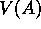 as 0. This is the
answer that batch Monte Carlo methods give. Notice that it is also the answer that
gives minimum squared error on the training data. In fact, it gives zero error on the
data. But still we expect the first answer to be better. If the process is Markov,
we expect that the first answer will produce lower error on future data, even
though the MC answer is better on the existing data.
as 0. This is the
answer that batch Monte Carlo methods give. Notice that it is also the answer that
gives minimum squared error on the training data. In fact, it gives zero error on the
data. But still we expect the first answer to be better. If the process is Markov,
we expect that the first answer will produce lower error on future data, even
though the MC answer is better on the existing data. 
The above example illustrates a general difference between the estimates found
by batch TD(0) and batch Monte Carlo methods. Batch Monte Carlo methods always find
the estimates that minimize mean squared error on the training set, whereas batch
TD(0) always finds the estimates that would be exactly correct for the
maximum-likelihood model of the Markov process. In general, the
maximum-likelihood estimate of a parameter is the parameter value whose
probability of generating the data is greatest. In this case, the maximum-likelihood
estimate is simply the model of the Markov process formed in the obvious way from the
observed episodes: the estimated transition probability from i to
j is just the fraction of observed transitions from i that went to j, and
the associated expected reward is just the average of the rewards observed on
those transitions. Given this model, we can compute the the estimate of the
value function that would be exactly correct if the model were exactly correct.
This is called the certainty-equivalence estimate because it is equivalent
to assuming that the estimate of the underlying process was known with certainty
rather than being approximated. In general, batch TD(0) converges to the
certainty-equivalence estimate.
This helps explain why TD methods converge more quickly than MC methods. In batch
form, TD(0) is faster than Monte Carlo methods because it computes the
true certainty-equivalence estimate. This explains the advantage of TD(0) shown
in the batch results on the random-walk task (Figure 6.8). The
relationship to the certainty-equivalence estimate may also explain in part the speed
advantage of non-batch TD(0) (e.g., Figure 6.7). Although the
non-batch methods do not achieve either the certainty-equivalence or the
minimum-squared-error estimates, they can be understood as moving roughly in these
directions. Non-batch TD(0) may be faster than constant-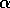 MC
simply because it is moving towards a better estimate, even though it is not
getting all the way there. At the current time nothing more definite can be said
about the relative efficiency of online TD and MC methods.
MC
simply because it is moving towards a better estimate, even though it is not
getting all the way there. At the current time nothing more definite can be said
about the relative efficiency of online TD and MC methods.
Finally, it is worth noting that although the certainty-equivalence estimate is
in some sense an optimal solution, it is almost never feasible to compute it
directly. If N is the number of states, then simply forming the
maximum-likelihood estimate of the process may require 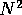 memory, and
computing the corresponding value function requires on the order of
memory, and
computing the corresponding value function requires on the order of 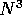 computational steps if done conventionally. In these terms it is indeed
striking that TD methods can approximate the same solution using memory no
more than N and repeated computations over the training set. On tasks with
large state spaces, TD methods may be the only feasible way of approximating the
certainty-equivalence solution.
computational steps if done conventionally. In these terms it is indeed
striking that TD methods can approximate the same solution using memory no
more than N and repeated computations over the training set. On tasks with
large state spaces, TD methods may be the only feasible way of approximating the
certainty-equivalence solution.



Next: 6.4 Sarsa: On-Policy TD
Up: 6 Temporal Difference Learning
Previous: 6.2 Advantages of TD
Richard Sutton
Fri May 30 13:53:05 EDT 1997
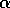 , as long as
, as long as 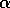 is chosen to be sufficiently small.
The constant-
is chosen to be sufficiently small.
The constant-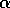 MC method also converges deterministically under the same
conditions, but to a different answer.
Understanding these two answers will help us understand the difference between
the two methods. Under normal updating the methods do not move all the way to
their respective batch answers, but in some sense they take a step in these
directions. Before trying to understand the two answers in general, for all
possible tasks, we first look at a few examples.
MC method also converges deterministically under the same
conditions, but to a different answer.
Understanding these two answers will help us understand the difference between
the two methods. Under normal updating the methods do not move all the way to
their respective batch answers, but in some sense they take a step in these
directions. Before trying to understand the two answers in general, for all
possible tasks, we first look at a few examples.



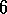 .
.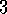 Random walk under batch updating.
Batch-updating versions of TD(0) and constant-
Random walk under batch updating.
Batch-updating versions of TD(0) and constant-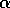 MC were applied as follows
to the random-walk prediction example (Example 6
.2). After each new
episode, all episodes seen so far were treated as a batch. They were
repeatedly presented to the algorithm, either TD(0) or constant-
MC were applied as follows
to the random-walk prediction example (Example 6
.2). After each new
episode, all episodes seen so far were treated as a batch. They were
repeatedly presented to the algorithm, either TD(0) or constant-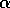 MC, with
MC, with 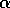 \
sufficiently small that the value function converged.
The resulting value function was then compared to
\
sufficiently small that the value function converged.
The resulting value function was then compared to 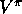 , and the
average mean-squared error across the five states (and across 100 independent
repetitions of the whole experiment) was plotted to obtain the learning curves
shown in Figure
, and the
average mean-squared error across the five states (and across 100 independent
repetitions of the whole experiment) was plotted to obtain the learning curves
shown in Figure 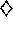

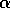 MC under batch training on the
random-walk task.
MC under batch training on the
random-walk task.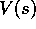 , that are the
sample averages of the actual returns experienced after visiting each state
s. These are optimal estimates in the sense that they minimize the mean-squared
error from the actual returns in the training set. In this sense it is surprising
that the batch TD method was able to perform better in the mean-squared error measure
shown in Figure
, that are the
sample averages of the actual returns experienced after visiting each state
s. These are optimal estimates in the sense that they minimize the mean-squared
error from the actual returns in the training set. In this sense it is surprising
that the batch TD method was able to perform better in the mean-squared error measure
shown in Figure 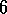 .
.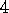 You are the Predictor.
Place yourself now in the role of the predictor of returns for a Markov
chain. Suppose you observe the following eight episodes:
You are the Predictor.
Place yourself now in the role of the predictor of returns for a Markov
chain. Suppose you observe the following eight episodes:
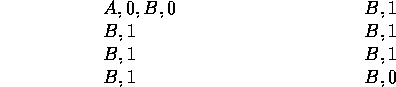
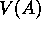 and
and 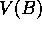 ? Everyone would probably agree that the optimal value for
? Everyone would probably agree that the optimal value for
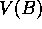 is
is 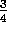 , because six out of the eight times in state
B the process terminated immediately with a return of 1, and the other two times
in B the process terminated immediately with a return of 0.
, because six out of the eight times in state
B the process terminated immediately with a return of 1, and the other two times
in B the process terminated immediately with a return of 0.
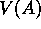 given this data? Here there are
two reasonable answers. One is to observe that 100% of the times the process was in
state A it traversed immediately to B (with a reward of 0), and we
have already decided that B has value
given this data? Here there are
two reasonable answers. One is to observe that 100% of the times the process was in
state A it traversed immediately to B (with a reward of 0), and we
have already decided that B has value 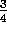 , so therefore A must have value
, so therefore A must have value
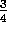 as well. One way of viewing this answer is that it is based on first
modeling the Markov process, in this case as
as well. One way of viewing this answer is that it is based on first
modeling the Markov process, in this case as

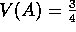 . This is also the answer that batch TD(0) gives.
. This is also the answer that batch TD(0) gives.
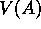 as 0. This is the
answer that batch Monte Carlo methods give. Notice that it is also the answer that
gives minimum squared error on the training data. In fact, it gives zero error on the
data. But still we expect the first answer to be better. If the process is Markov,
we expect that the first answer will produce lower error on future data, even
though the MC answer is better on the existing data.
as 0. This is the
answer that batch Monte Carlo methods give. Notice that it is also the answer that
gives minimum squared error on the training data. In fact, it gives zero error on the
data. But still we expect the first answer to be better. If the process is Markov,
we expect that the first answer will produce lower error on future data, even
though the MC answer is better on the existing data. 
 MC
simply because it is moving towards a better estimate, even though it is not
getting all the way there. At the current time nothing more definite can be said
about the relative efficiency of online TD and MC methods.
MC
simply because it is moving towards a better estimate, even though it is not
getting all the way there. At the current time nothing more definite can be said
about the relative efficiency of online TD and MC methods.
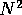 memory, and
computing the corresponding value function requires on the order of
memory, and
computing the corresponding value function requires on the order of 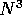 computational steps if done conventionally. In these terms it is indeed
striking that TD methods can approximate the same solution using memory no
more than N and repeated computations over the training set. On tasks with
large state spaces, TD methods may be the only feasible way of approximating the
certainty-equivalence solution.
computational steps if done conventionally. In these terms it is indeed
striking that TD methods can approximate the same solution using memory no
more than N and repeated computations over the training set. On tasks with
large state spaces, TD methods may be the only feasible way of approximating the
certainty-equivalence solution.