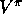 or
or 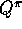 , but all we have
are episodes following
, but all we have
are episodes following 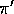 , where
, where 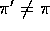 . Can we do it?
. Can we do it?



So far we have considered methods for estimating the value functions for a
policy given an infinite supply of episodes generated using that policy.
Suppose now that all we have are episodes generated from a different policy.
That is, suppose we wish to estimate 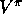 or
or 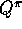 , but all we have
are episodes following
, but all we have
are episodes following 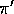 , where
, where 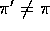 . Can we do it?
. Can we do it?
Happily, in many cases we can. Of course, in order to use episodes from 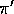 to estimate values for
to estimate values for  , we require that every action taken under
, we require that every action taken under  is also taken, at least occasionally, under
is also taken, at least occasionally, under 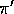 . That is, we require
that
. That is, we require
that 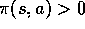 imply
imply
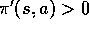 . In the episodes generated using
. In the episodes generated using 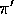 , consider the
ith first visit to state s and the complete sequence of states and actions
following that visit. Let
, consider the
ith first visit to state s and the complete sequence of states and actions
following that visit. Let 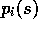 and
and
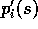 denote the probabilities of that complete sequence happening given
policies
denote the probabilities of that complete sequence happening given
policies  and
and 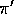 and starting from s. Let
and starting from s. Let 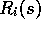 denote the corresponding observed return from state s. To average
these to obtain an unbiased estimate of
denote the corresponding observed return from state s. To average
these to obtain an unbiased estimate of 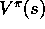 , we need only weight each
return by its relative probability of occurring under
, we need only weight each
return by its relative probability of occurring under  and
and 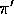 , that
is, by
, that
is, by
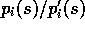 . The desired Monte Carlo estimate after observing
. The desired Monte Carlo estimate after observing 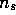 returns from state s is then
returns from state s is then
This equation involves the probabilities 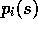 and
and 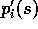 ,
which are normally considered unknown in applications of Monte Carlo methods.
Fortunately, here we need only their ratio,
,
which are normally considered unknown in applications of Monte Carlo methods.
Fortunately, here we need only their ratio, 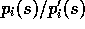 , which
can be determined with no knowledge of the environment's dynamics. Let
, which
can be determined with no knowledge of the environment's dynamics. Let
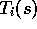 be the time of termination of the i th episode involving state
s. Then
be the time of termination of the i th episode involving state
s. Then
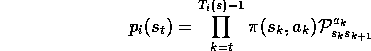
and
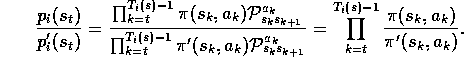
Thus the weight needed in (5.3), 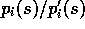 , depends
only on the two policies and not at all on the environment's dynamics.
, depends
only on the two policies and not at all on the environment's dynamics.
Exercise 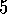 .
.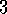
What is the Monte Carlo estimate analogous to (5.3) for
action values, given returns generated using 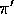 ?
?


