


Next: 4.1 Policy Evaluation
Up: Contents
Previous: Part II:
Elementary Solution Methods
The term ``Dynamic Programming" (DP) refers to a collection of algorithms that
can be used to compute optimal policies given a perfect model of the environment
as a Markov decision process (MDP). Classical DP algorithms are of limited
utility in reinforcement learning both because of their assumption of a perfect
model and because of their great computational expense, but they are still very
important theoretically. DP provides an essential foundation for the
understanding of the methods presented in the rest of this book. In fact, all of
these methods can be viewed as attempts to achieve much the same effect as DP,
only with less computation and without assuming a perfect model of the environment.
Starting with this chapter, we usually assume that the environment is a
finite MDP. That is, we assume that its state and action sets, 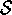 and
and 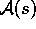 , for
, for 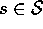 , are finite, and that its dynamics are given by a set of
transition probabilities,
, are finite, and that its dynamics are given by a set of
transition probabilities,
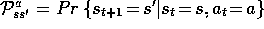 , and expected
immediate rewards,
, and expected
immediate rewards,
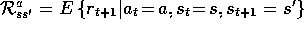 , for all
, for all 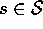 ,
,
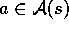 , and
, and 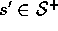 (
(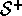 is
is 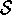 plus a terminal state if the
problem is episodic). Although DP ideas can be applied to problems
with continuous state and action spaces, exact
solutions are possible only in special cases. A common way of obtaining
approximate solutions for continuous state and action tasks is to quantize the
state and action spaces and then apply finite-state DP methods. The methods we
explore in Chapter 8 are applicable to continuous problems and are a significant
extension of that approach.
plus a terminal state if the
problem is episodic). Although DP ideas can be applied to problems
with continuous state and action spaces, exact
solutions are possible only in special cases. A common way of obtaining
approximate solutions for continuous state and action tasks is to quantize the
state and action spaces and then apply finite-state DP methods. The methods we
explore in Chapter 8 are applicable to continuous problems and are a significant
extension of that approach.
The key idea of DP, and of reinforcement learning generally, is the
use of value functions to organize and structure the search for good policies. In
this chapter we show how DP can be used to compute the value
functions defined in Chapter 3. As discussed there, we can easily
obtain optimal policies once we have found the optimal value functions, 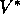 or
or
 , which satisfy the Bellman optimality equations:
, which satisfy the Bellman optimality equations:

or
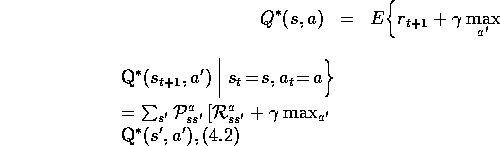
for all 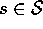 ,
, 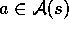 , and
, and 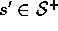 .
As we shall see, DP algorithms are obtained by
turning Bellman equations such as these into assignment statements, that
is, into update rules for improving approximations of the desired
value functions.
.
As we shall see, DP algorithms are obtained by
turning Bellman equations such as these into assignment statements, that
is, into update rules for improving approximations of the desired
value functions.



Next: 4.1 Policy Evaluation
Up: Contents
Previous: Part II:
Elementary Solution Methods
Richard Sutton
Fri May 30 12:39:34 EDT 1997
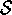 and
and 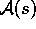 , for
, for 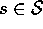 , are finite, and that its dynamics are given by a set of
transition probabilities,
, are finite, and that its dynamics are given by a set of
transition probabilities,
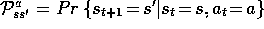 , and expected
immediate rewards,
, and expected
immediate rewards,
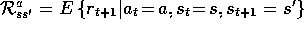 , for all
, for all 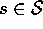 ,
,
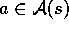 , and
, and 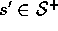 (
(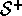 is
is 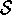 plus a terminal state if the
problem is episodic). Although DP ideas can be applied to problems
with continuous state and action spaces, exact
solutions are possible only in special cases. A common way of obtaining
approximate solutions for continuous state and action tasks is to quantize the
state and action spaces and then apply finite-state DP methods. The methods we
explore in Chapter 8 are applicable to continuous problems and are a significant
extension of that approach.
plus a terminal state if the
problem is episodic). Although DP ideas can be applied to problems
with continuous state and action spaces, exact
solutions are possible only in special cases. A common way of obtaining
approximate solutions for continuous state and action tasks is to quantize the
state and action spaces and then apply finite-state DP methods. The methods we
explore in Chapter 8 are applicable to continuous problems and are a significant
extension of that approach.



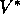 or
or
 , which satisfy the Bellman optimality equations:
, which satisfy the Bellman optimality equations:

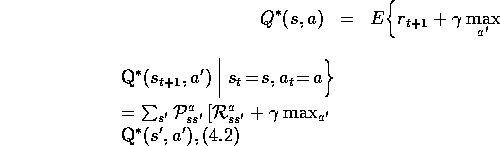
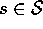 ,
, 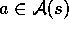 , and
, and 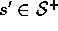 .
As we shall see, DP algorithms are obtained by
turning Bellman equations such as these into assignment statements, that
is, into update rules for improving approximations of the desired
value functions.
.
As we shall see, DP algorithms are obtained by
turning Bellman equations such as these into assignment statements, that
is, into update rules for improving approximations of the desired
value functions.