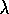10.1 The Unified View

All of the reinforcement learning methods we have explored in this book have three key ideas in common. First, the objective of all of them is the estimation of value functions. Second, all operate by backing up values along actual or possible state trajectories. Third, all follow the general strategy of generalized policy iteration (GPI), meaning that they maintain an approximate value function and an approximate policy, and they continually try to improve each on the basis of the other. These three ideas that the our methods have in common circumscribe the subject covered in this book. We suggest that value functions, backups, and GPI are powerful organizing principles potentially relevant to any model of intelligence.

Two of the most important dimensions along which the methods vary are shown in Figure 10.1. These dimensions have to do with the kind of backup used to improve the value function. The vertical dimension is whether they are sample backups (based on a sample trajectory) or full backups (based on a distribution of possible trajectories). Full backups of course require a model, whereas sample backups can be done either with or without a model (another dimension of variation). The horizontal dimension corresponds to the depth of backups, i.e., to the degree of bootstrapping. At three of the four corners of the space are the three primary methods for estimating values: DP, TD, and Monte Carlo methods. Along the lower edge of the space are the sample-backup methods, ranging from 1-step TD backups to full-return Monte Carlo backups. Between these is a spectrum including methods based on n -step backups and mixtures of n -step backups such as the 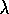-backups implemented by eligibility traces.

  
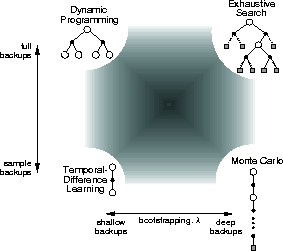
Figure 10.1: A slice of the space of reinforcement learning methods.

DP methods are shown in the extreme upper-left corner of the space because they involve 1-step full backups. The upper-right corner is the extreme case of full backups so deep that they run all the way to terminal states (or, in a continual problem, until discounting has reduced the contribution of any further rewards to a negligible level). This is the case of exhaustive search. Intermediate methods along this dimension include heuristic search and related methods that search and backup up to a limited depth, perhaps selectively. There are also methods that are intermediate along the vertical dimension. These include methods that mix full and sample backups, such as Dyna, as well as the possibility of methods that mix samples and distributions within a single backup. The interior of the square is filled in to represent the space of all such intermediate methods.

A third important dimension is that of function approximation. Function approximation can be viewed as an orthogonal spectrum of possibilities ranging from tabular methods at one extreme through state aggregation, a variety of linear methods, and then a diverse set of nonlinear methods. This third dimension might be visualized as perpendicular to the plane of the page in Figure 10.1.

Another dimension that we heavily emphasized in this book is the binary distinction between on-policy and off-policy methods. In the former case, the agent learns the value function for the policy it is currently following, whereas in the latter case it learns the value function for the policy that it currently thinks is best. These two policies are often different because of the need to explore. The interaction between this dimension and the bootstrapping and function approximation dimension discussed in Chapter 8 illustrates the advantages of analyzing the space of methods in terms of dimensions. Even though this did involve an interaction between three dimensions, many other dimensions were found to be irrelevant, greatly simplifying the analysis and increasing its significance.

In addition to the four dimensions just discussed, we have identified a number of others throughout the book, including:

definition of return

Is the task episodic or continual, discounted or undiscounted?

action values vs. state values

What kind of values should be estimated? If only state values are estimated, then either a model or a separate policy (as in actor-critic methods) is required for action selection.

action selection/exploration

How are actions selected to ensure a suitable tradeoff between exploration and exploitation? We have considered only the simplest ways to do this: -greedy and softmax action selection, and optimistic initialization of values.

synchronous vs. asynchronous

Are the backups for all states performed simultaneously or one-by-one in some order?

replacing vs. accumulating traces

If eligibility traces are used, which kind is most appropriate?

real vs. simulated

Should one backup real experience or simulated experience? If both, how much of each?

location of backups

What states or state-actions pairs should be backed up? Model-free methods can choose only among the states and state-action pairs actually encountered, but model-based methods can choose arbitrarily. There are many potent possibilities here.

timing of backups

Should backups be done as part of selecting actions, or only afterward?

Of course, these dimensions are neither exhaustive nor mutually exclusive. Individual algorithms differ in many other ways as well, and many algorithms lie in several places along several dimensions. For example, Dyna methods use both real and simulated experience to affect the same value function. It is also perfectly sensible to maintain multiple value functions computed in different ways or over different state and action representations. These dimensions do, however, constitute a coherent set of ideas for describing and exploring a wide space of possible algorithms.