


Next: 6.8 Games, Afterstates, and
Up: 6. Temporal-Difference Learning
Previous: 6.6 Actor-Critic Methods
Contents
R-learning is an off-policy control method for the advanced version of the
reinforcement learning problem in which one neither discounts nor divides
experience into distinct episodes with finite returns. In this case one seeks
to obtain the maximum reward per time step. The
value functions for a policy,  , are defined relative to the
average expected reward per time step under the policy,
, are defined relative to the
average expected reward per time step under the policy, 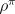 :
:
assuming the process is ergodic (nonzero probability of reaching any
state from any other under any policy) and thus that 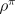 does
not depend on the starting state. From any state, in the long run the average
reward is the same, but there is a transient. From some states
better-than-average rewards are received for a while, and from others
worse-than-average rewards are received. It is this transient that defines the value
of a state:
does
not depend on the starting state. From any state, in the long run the average
reward is the same, but there is a transient. From some states
better-than-average rewards are received for a while, and from others
worse-than-average rewards are received. It is this transient that defines the value
of a state:
and the value of a state-action pair is similarly the transient difference in
reward when starting in that state and taking that action:
We call these relative values because they are
relative to the average reward under the current policy.
There are subtle distinctions that need to be drawn between different kinds
of optimality in the undiscounted continuing case. Nevertheless, for most practical
purposes it may be adequate simply to order policies according to their average
reward per time step, in other words, according to their 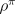 . For now
let us consider all policies that attain the maximal value of
. For now
let us consider all policies that attain the maximal value of 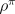 to be
optimal.
to be
optimal.
Other than its use of relative values, R-learning is a standard TD control
method based on off-policy GPI, much like Q-learning. It maintains two policies, a
behavior policy and an estimation policy, plus an action-value function and an
estimated average reward. The behavior policy is used to generate experience;
it might be the 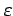 -greedy policy with respect to the action-value
function. The estimation policy is the one involved in GPI. It is typically the
greedy policy with respect to the action-value function. If
-greedy policy with respect to the action-value
function. The estimation policy is the one involved in GPI. It is typically the
greedy policy with respect to the action-value function. If  is the estimation
policy, then the action-value function,
is the estimation
policy, then the action-value function, 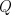 , is an approximation of
, is an approximation of 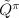 and the average reward,
and the average reward, 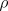 , is an approximation of
, is an approximation of 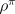 . The
complete algorithm is given in Figure
6.16. There has been
little experience with this method and it should be considered experimental.
. The
complete algorithm is given in Figure
6.16. There has been
little experience with this method and it should be considered experimental.
Figure
6.16:
R-learning: An off-policy TD control algorithm for undiscounted,
continuing tasks. The scalars 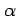 and
and 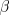 are step-size parameters.
are step-size parameters.

|
Example 6.7: An Access-Control Queuing Task
This is a decision task involving access control to a set of  servers. Customers of
four different priorities arrive at a single queue. If given access to a server,
the customers pay a reward of 1, 2, 4, or 8, depending on their priority, with
higher priority customers paying more. In each time step, the customer at the head of
the queue is either accepted (assigned to one of the servers) or rejected (removed
from the queue). In either case, on the next time step the next customer in the
queue is considered. The queue never empties, and the proportion of (randomly
distributed) high priority customers in the queue is
servers. Customers of
four different priorities arrive at a single queue. If given access to a server,
the customers pay a reward of 1, 2, 4, or 8, depending on their priority, with
higher priority customers paying more. In each time step, the customer at the head of
the queue is either accepted (assigned to one of the servers) or rejected (removed
from the queue). In either case, on the next time step the next customer in the
queue is considered. The queue never empties, and the proportion of (randomly
distributed) high priority customers in the queue is 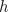 . Of course a customer can
be served only if there is a free server. Each busy server becomes free with
probability
. Of course a customer can
be served only if there is a free server. Each busy server becomes free with
probability
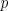 on each time step. Although we have just described them for definiteness, let us
assume the statistics of arrivals and departures are unknown. The task is to decide on
each step whether to accept or reject the next customer, on the basis of his priority
and the number of free servers, so as to maximize long-term reward without
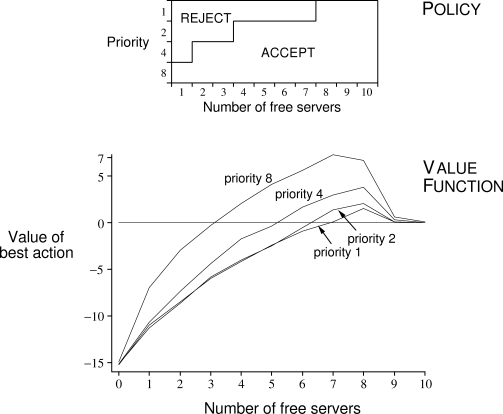
discounting. Figure
6.17 shows the solution found by R-learning for
this task with
on each time step. Although we have just described them for definiteness, let us
assume the statistics of arrivals and departures are unknown. The task is to decide on
each step whether to accept or reject the next customer, on the basis of his priority
and the number of free servers, so as to maximize long-term reward without
discounting. Figure
6.17 shows the solution found by R-learning for
this task with 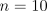 ,
, 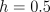 , and
, and 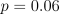 . The R-learning
parameters were
. The R-learning
parameters were 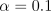 ,
,
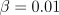 , and
, and 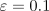 . The initial action values and
. The initial action values and 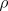 were zero.
were zero.
Figure
6.17:
The policy and value function found by R-learning on the
access-control queuing task after 2 million steps. The drop on the right of the
graph is probably due to insufficient data; many of these states were never
experienced. The value learned for 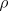 was about
was about 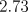 .
.
|
 Exercise 6.11
Design an on-policy method for undiscounted, continuing tasks.
Exercise 6.11
Design an on-policy method for undiscounted, continuing tasks.



Next: 6.8 Games, Afterstates, and
Up: 6. Temporal-Difference Learning
Previous: 6.6 Actor-Critic Methods
Contents
Mark Lee
2005-01-04
![]() , are defined relative to the
average expected reward per time step under the policy,
, are defined relative to the
average expected reward per time step under the policy, ![]() :
:
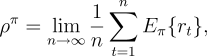
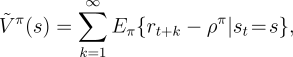
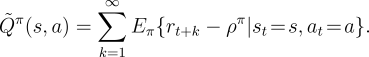
![]() . For now
let us consider all policies that attain the maximal value of
. For now
let us consider all policies that attain the maximal value of ![]() to be
optimal.
to be
optimal.
![]() -greedy policy with respect to the action-value
function. The estimation policy is the one involved in GPI. It is typically the
greedy policy with respect to the action-value function. If
-greedy policy with respect to the action-value
function. The estimation policy is the one involved in GPI. It is typically the
greedy policy with respect to the action-value function. If ![]() is the estimation
policy, then the action-value function,
is the estimation
policy, then the action-value function, ![]() , is an approximation of
, is an approximation of ![]() and the average reward,
and the average reward, ![]() , is an approximation of
, is an approximation of ![]() . The
complete algorithm is given in Figure
6.16. There has been
little experience with this method and it should be considered experimental.
. The
complete algorithm is given in Figure
6.16. There has been
little experience with this method and it should be considered experimental.


 Exercise 6.11
Design an on-policy method for undiscounted, continuing tasks.
Exercise 6.11
Design an on-policy method for undiscounted, continuing tasks.