6.5 Q-learning: Off-Policy TD Control

One of the most important breakthroughs in reinforcement learning was the development of an off-policy TD control algorithm known as Q-learning (Watkins, 1989). Its simplest form, 1-step Q-learning is defined by

In this case, the learned action-value function, Q, directly approximates 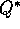, the optimal action-value function, independent of the policy being followed. This dramatically simplifies the analysis of the algorithm and enabled early convergence proofs. The policy still has an effect in that it determines which state-action pairs are visited and updated. However, all that is required for correct convergence is that all pairs continue to be updated. As we have discussed before, this is a minimal requirement in the sense that any method guaranteed to find optimal behavior in the general case must require it. Under this assumption and a variant of the usual stochastic approximation conditions on the step-size sequence, has been shown to converge with probability one to 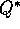. The Q-learning algorithm is shown in procedural form in Figure 6.12.

Initialize  arbitrarily
Repeat (for each episode):
   Initialize s
   Repeat (for each step of episode):
      Choose a from s using policy derived from Q
         (e.g., -greedy)
      Take action a, observe r, 
      
      ;
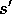
   until s is terminal

What is the backup diagram for Q-learning? The rule (6.6) updates a state-action pair, so the top node, the root of the backup, must be a small, filled action node. The backup is also from action nodes, maximizing over all those actions possible in the next state. Thus the bottom nodes of the backup diagram should be all these action nodes. Finally, remember that we indicate taking the maximum of these ``next action" nodes with an arc across them (Figure 3 .7 ). Can you guess now what the diagram is? If so, please do make a guess before turning to the answer (on the next page) in Figure 6.14.

  
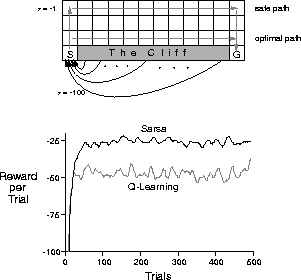
Figure 6.13: The cliff-walking task. Off-policy Q-learning learns the optimal policy, along the edge of the cliff, but then keeps falling off because of the -greedy action selection. On-policy Sarsa learns a safer policy taking into account the action selection method. These data are from a single run, but smoothed.

  
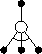
Figure 6.14: The backup diagram for Q-learning.

Example 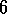. Cliff Walking. This gridworld example compares Sarsa and Q-learning, highlighting the difference between on-policy (Sarsa) and off-policy (Q-learning) methods. Consider the gridworld shown in the upper part of Figure 6.13. This is a standard undiscounted, episodic task, with start and goal states, and the usual actions causing movement up, down, right, and left. Reward is -1 on all transitions except into the the region marked ``The Cliff." Stepping into this region incurs a reward of -100 and sends the agent instantly back to the start. The lower part of the figure shows the performance of the Sarsa and Q-learning methods with -greedy action selection, . After an initial transient, Q-learning learns values for the optimal policy, that which travels right along the edge of the cliff. Unfortunately, this results in it occasionally falling off the cliff because of the -greedy action selection. Sarsa, on the other hand, takes into account the action selection and learns the longer but safer path through the upper part of the grid. Although Q-learning actually learns the values of the optimal policy, its online performance is worse than that of Sarsa, which learns the roundabout policy. Of course, if were gradually reduced, then both methods would asymptotically converge to the optimal policy.

Exercise .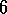

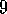
Why is Q-learning considered an off-policy control method?

Exercise .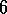

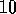
Consider the learning algorithm that is just like Q-learning except that instead of the maximum over next state-action pairs it uses the expected value, taking into account how likely each action is under the current policy. That is, consider the algorithm otherwise like Q-learning except with the update rule

Is this new method an on-policy or off-policy method? What is the backup diagram for this algorithm? Given the same amount of experience, would you expect this method to work better or worse than Sarsa? What other considerations might impact the comparison of this method with Sarsa?