


Next: 4.8 Summary
Up: 4 Dynamic Programming
Previous: 4.6 Generalized Policy Iteration
DP may not be practical for very large problems, but, compared to other
methods for solving MDPs, DP is actually quite efficient. If we ignore
a few technical details, then the (worst case) time they take to find an
optimal policy is polynomial in the number of states and actions. If n
and m respectively denote the number of states and actions, this means
that a DP algorithm takes a number of computational operations that is
less than some polynomial function of n and m. A DP algorithm is
guaranteed to find an optimal policy in polynomial time even though the
total number of (deterministic) policies is 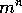 . In this sense, DP is
exponentially faster than any direct search in policy space could be,
because direct search would have to exhaustively examine each policy to
provide the same guarantee. Linear-programming methods can also be used to solve
MDPs, and in some cases their worst-case convergence guarantees are better than
those of DP methods. But linear-programming methods become impractical at a much
smaller number of states than DP methods (by a factor of about one hundred). For
the largest problems, only DP methods are feasible.
. In this sense, DP is
exponentially faster than any direct search in policy space could be,
because direct search would have to exhaustively examine each policy to
provide the same guarantee. Linear-programming methods can also be used to solve
MDPs, and in some cases their worst-case convergence guarantees are better than
those of DP methods. But linear-programming methods become impractical at a much
smaller number of states than DP methods (by a factor of about one hundred). For
the largest problems, only DP methods are feasible.
DP is sometimes thought to be of limited applicability because of the curse of
dimensionality
(Bellman, 1957), the fact that the number of states often grows exponentially with
the number of state variables. Large state sets do create difficulties, but these
are inherent difficulties of the problem, not of DP as a solution method. In
fact, DP is comparatively better suited to handling very large state spaces than
competitor methods such as direct search and linear programming.
In practice, DP methods can be used with today's computers to solve MDPs with
millions of states. Both policy iteration and value iteration are widely used,
and it is not clear which if either is better in general. In practice, these
methods usually converge much faster their theoretical worst-case run-times,
particularly if they are started with good initial value functions or policies.
On problems with very large state spaces, asynchronous DP methods are
generally prefered. To complete even one sweep of a synchronous method requires
computation and memory for every state. For some problems, even this much memory
and computation is impractical, yet the problem is still potentially solvable
because only a relatively few states occur along optimal solution trajectories.
Asynchronous methods and other variations of GPI can often be applied in such cases
to find good or optimal policies much faster than synchronous methods.



Next: 4.8 Summary
Up: 4 Dynamic Programming
Previous: 4.6 Generalized Policy Iteration
Richard Sutton
Sat May 31 11:09:21 EDT 1997
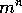 . In this sense, DP is
exponentially faster than any direct search in policy space could be,
because direct search would have to exhaustively examine each policy to
provide the same guarantee. Linear-programming methods can also be used to solve
MDPs, and in some cases their worst-case convergence guarantees are better than
those of DP methods. But linear-programming methods become impractical at a much
smaller number of states than DP methods (by a factor of about one hundred). For
the largest problems, only DP methods are feasible.
. In this sense, DP is
exponentially faster than any direct search in policy space could be,
because direct search would have to exhaustively examine each policy to
provide the same guarantee. Linear-programming methods can also be used to solve
MDPs, and in some cases their worst-case convergence guarantees are better than
those of DP methods. But linear-programming methods become impractical at a much
smaller number of states than DP methods (by a factor of about one hundred). For
the largest problems, only DP methods are feasible.


