


Next: 7.5 Sarsa(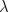 )
Up: 7. Eligibility Traces
Previous: 7.3 The Backward View
Contents
)
Up: 7. Eligibility Traces
Previous: 7.3 The Backward View
Contents
In this section we show that off-line TD( ), as defined
mechanistically above, achieves the same weight updates as the off-line
), as defined
mechanistically above, achieves the same weight updates as the off-line  -return
algorithm. In this sense we align the forward (theoretical) and
backward (mechanistic) views of
TD(
-return
algorithm. In this sense we align the forward (theoretical) and
backward (mechanistic) views of
TD( ). Let
). Let 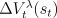 denote the update at time
denote the update at time  of
of 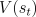 according to the
according to the
 -return algorithm (7.4), and let
-return algorithm (7.4), and let 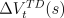 denote the update
at time
denote the update
at time  of state
of state  according to the mechanistic definition of TD(
according to the mechanistic definition of TD( ) as
given by (7.7). Then our goal is to
show that the sum of all the updates over an episode is the same for the two
algorithms:
) as
given by (7.7). Then our goal is to
show that the sum of all the updates over an episode is the same for the two
algorithms:
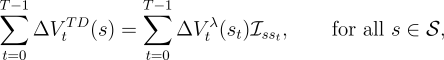
| (7.8) |
where 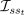 is an identity indicator function, equal to
is an identity indicator function, equal to 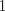 if
if 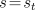 and equal to 0 otherwise.
and equal to 0 otherwise.
First note that an accumulating eligibility trace can be written
explicitly (nonrecursively) as
Thus, the left-hand side of (7.8) can be written
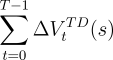
| 
| 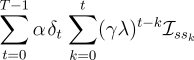
| (7.9) | | | 
| 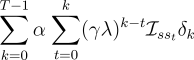
| (7.10) | | | 
| 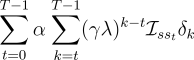
| (7.11) | | | 
| 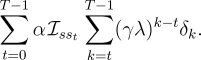
| (7.12) | |
Now we turn to the right-hand side of (7.8).
Consider an individual update of the  -return algorithm:
-return algorithm:
Examine the first column inside the brackets--all the 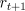 's with
their weighting factors of
's with
their weighting factors of 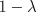 times powers of
times powers of  . It turns out that all the
weighting factors sum to 1. Thus we can pull out the first column and get
an unweighted term of
. It turns out that all the
weighting factors sum to 1. Thus we can pull out the first column and get
an unweighted term of 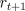 . A similar trick pulls out the second column in
brackets, starting from the second row, which sums to
. A similar trick pulls out the second column in
brackets, starting from the second row, which sums to 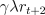 . Repeating
this for each column, we get
. Repeating
this for each column, we get
The approximation above is exact in the case of off-line updating, in which case
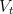 is the same for all
is the same for all  . The last step is exact (not an approximation)
because all the
. The last step is exact (not an approximation)
because all the
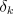 terms omitted are due to fictitious steps "after" the terminal state has been
entered. All these steps have zero rewards and zero values; thus all their
terms omitted are due to fictitious steps "after" the terminal state has been
entered. All these steps have zero rewards and zero values; thus all their
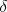 's are zero as well. Thus, we have shown that in the off-line case the
right-hand side of (7.8) can be written
's are zero as well. Thus, we have shown that in the off-line case the
right-hand side of (7.8) can be written
which is the same as (7.9). This proves (7.8).
In the case of on-line updating, the approximation made above will be close as
long as 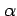 is small and thus
is small and thus 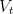 changes little during an episode. Even in
the on-line case we can expect the updates of TD(
changes little during an episode. Even in
the on-line case we can expect the updates of TD( ) and of the
) and of the  -return algorithm
to be similar.
-return algorithm
to be similar.
For the moment let us assume that the increments are small
enough during an episode that on-line TD( ) gives essentially the same update over
the course of an episode as does the
) gives essentially the same update over
the course of an episode as does the  -return algorithm. There still remain
interesting questions about what happens during an episode. Consider the
updating of the value of state
-return algorithm. There still remain
interesting questions about what happens during an episode. Consider the
updating of the value of state 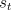 in midepisode, at time
in midepisode, at time 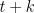 . Under on-line
TD(
. Under on-line
TD( ), the effect at
), the effect at 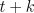 is just as if we had done a
is just as if we had done a  -return update treating
the last observed state as the terminal state of the episode with a nonzero
terminal value equal to its current estimated value. This relationship is
maintained from step to step as each new state is observed.
-return update treating
the last observed state as the terminal state of the episode with a nonzero
terminal value equal to its current estimated value. This relationship is
maintained from step to step as each new state is observed.
Example 7.3: Random Walk with TD( )
Because off-line TD(
)
Because off-line TD( ) is equivalent to the
) is equivalent to the  -return algorithm, we already have
the results for off-line TD(
-return algorithm, we already have
the results for off-line TD( ) on the 19-state random walk task; they are shown
in Figure
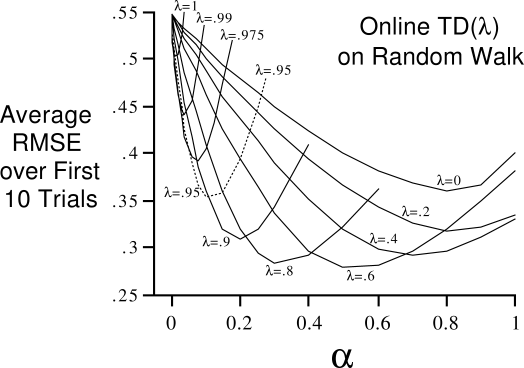
7.6. The comparable results for on-line TD(
) on the 19-state random walk task; they are shown
in Figure
7.6. The comparable results for on-line TD( ) are
shown in Figure
7.9. Note that the on-line algorithm works
better over a broader range of parameters. This is often found to be the case for
on-line methods.
) are
shown in Figure
7.9. Note that the on-line algorithm works
better over a broader range of parameters. This is often found to be the case for
on-line methods.
Figure
7.9:
Performance of on-line TD( ) on the 19-state random walk task.
) on the 19-state random walk task.
|
 Exercise 7.5
Although TD(
Exercise 7.5
Although TD( ) only approximates the
) only approximates the  -return
algorithm when done online, perhaps there's a slightly different TD method
that would maintain the equivalence even in the on-line case. One idea is to
define the TD error instead as
-return
algorithm when done online, perhaps there's a slightly different TD method
that would maintain the equivalence even in the on-line case. One idea is to
define the TD error instead as 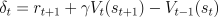 and the
and the  -step return as
-step return as 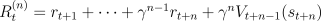 . Show that in this case the
modified TD(
. Show that in this case the
modified TD( ) algorithm would then achieve exactly
) algorithm would then achieve exactly
even in the case of on-line updating with large  . In what ways might
this modified TD(
. In what ways might
this modified TD( ) be better or worse than the conventional one described in
the text? Describe an experiment to assess the relative merits of the two
algorithms.
) be better or worse than the conventional one described in
the text? Describe an experiment to assess the relative merits of the two
algorithms.



Next: 7.5 Sarsa( )
Up: 7. Eligibility Traces
Previous: 7.3 The Backward View
Contents
Mark Lee
2005-01-04
)
Up: 7. Eligibility Traces
Previous: 7.3 The Backward View
Contents
Mark Lee
2005-01-04
![]() ), as defined
mechanistically above, achieves the same weight updates as the off-line
), as defined
mechanistically above, achieves the same weight updates as the off-line ![]() -return
algorithm. In this sense we align the forward (theoretical) and
backward (mechanistic) views of
TD(
-return
algorithm. In this sense we align the forward (theoretical) and
backward (mechanistic) views of
TD(![]() ). Let
). Let ![]() denote the update at time
denote the update at time ![]() of
of ![]() according to the
according to the
![]() -return algorithm (7.4), and let
-return algorithm (7.4), and let ![]() denote the update
at time
denote the update
at time ![]() of state
of state ![]() according to the mechanistic definition of TD(
according to the mechanistic definition of TD(![]() ) as
given by (7.7). Then our goal is to
show that the sum of all the updates over an episode is the same for the two
algorithms:
) as
given by (7.7). Then our goal is to
show that the sum of all the updates over an episode is the same for the two
algorithms:
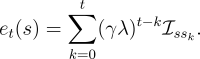
![]() -return algorithm:
-return algorithm:
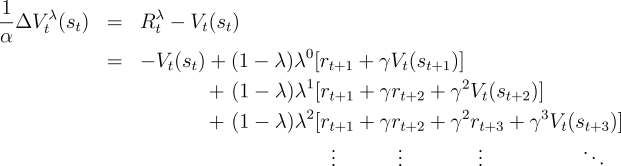
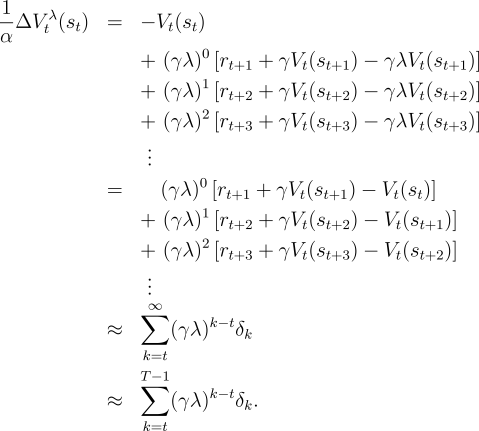
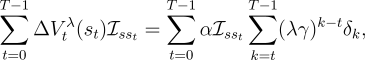
![]() is small and thus
is small and thus ![]() changes little during an episode. Even in
the on-line case we can expect the updates of TD(
changes little during an episode. Even in
the on-line case we can expect the updates of TD(![]() ) and of the
) and of the ![]() -return algorithm
to be similar.
-return algorithm
to be similar.
![]() ) gives essentially the same update over
the course of an episode as does the
) gives essentially the same update over
the course of an episode as does the ![]() -return algorithm. There still remain
interesting questions about what happens during an episode. Consider the
updating of the value of state
-return algorithm. There still remain
interesting questions about what happens during an episode. Consider the
updating of the value of state ![]() in midepisode, at time
in midepisode, at time ![]() . Under on-line
TD(
. Under on-line
TD(![]() ), the effect at
), the effect at ![]() is just as if we had done a
is just as if we had done a ![]() -return update treating
the last observed state as the terminal state of the episode with a nonzero
terminal value equal to its current estimated value. This relationship is
maintained from step to step as each new state is observed.
-return update treating
the last observed state as the terminal state of the episode with a nonzero
terminal value equal to its current estimated value. This relationship is
maintained from step to step as each new state is observed.

 Exercise 7.5
Although TD(
Exercise 7.5
Although TD(