How can we avoid the unlikely assumption of exploring starts? The only general way to ensure that all actions are selected infinitely often is for the agent to continue to select them. There are two approaches to ensuring this, resulting in what we call on-policy methods and off-policy methods. On-policy methods attempt to evaluate or improve the policy that is used to make decisions. In this section we present an on-policy Monte Carlo control method in order to illustrate the idea.
In on-policy control methods the policy is generally soft, meaning that
![]() for all
for all ![]() and all
and all ![]() . There are many
possible variations on on-policy methods. One possibility is to
gradually shift the policy toward a deterministic optimal policy.
Many of the methods discussed in Chapter 2 provide mechanisms
for this. The on-policy method we present in this section uses
. There are many
possible variations on on-policy methods. One possibility is to
gradually shift the policy toward a deterministic optimal policy.
Many of the methods discussed in Chapter 2 provide mechanisms
for this. The on-policy method we present in this section uses ![]() -greedy policies, meaning that most of the time they choose an action
that has maximal estimated action value, but with probability
-greedy policies, meaning that most of the time they choose an action
that has maximal estimated action value, but with probability ![]() they instead select an action at random. That is, all
nongreedy actions are given the minimal probability of selection,
they instead select an action at random. That is, all
nongreedy actions are given the minimal probability of selection,
![]() , and the remaining bulk of the probability,
, and the remaining bulk of the probability, ![]() , is given to the greedy action. The
, is given to the greedy action. The
![]() -greedy policies are examples of
-greedy policies are examples of ![]() -soft policies, defined as
policies for which
-soft policies, defined as
policies for which ![]() for all states and
actions, for some
for all states and
actions, for some ![]() . Among
. Among ![]() -soft policies,
-soft policies, ![]() -greedy
policies are in some sense those that are closest to greedy.
-greedy
policies are in some sense those that are closest to greedy.
The overall idea of on-policy Monte Carlo control is still that of
GPI. As in Monte Carlo ES, we use first-visit MC methods to
estimate the action-value function for the current policy. Without the
assumption of exploring starts, however, we cannot simply improve the policy
by making it greedy with respect to the current value function, because that
would prevent further exploration of nongreedy actions. Fortunately, GPI does
not require that the policy be taken all the way to a greedy
policy, only that it be moved toward a greedy policy. In our
on-policy method we will move it only to an ![]() -greedy policy. For any
-greedy policy. For any
![]() -soft policy,
-soft policy, ![]() , any
, any ![]() -greedy policy with respect to
-greedy policy with respect to ![]() is
guaranteed to be better than or equal to
is
guaranteed to be better than or equal to ![]() .
.
That any ![]() -greedy policy with respect to
-greedy policy with respect to ![]() is an improvement over any
is an improvement over any
![]() -soft policy
-soft policy ![]() is assured by the policy improvement theorem. Let
is assured by the policy improvement theorem. Let
![]() be the
be the ![]() -greedy policy. The conditions of the policy improvement
theorem apply because for any
-greedy policy. The conditions of the policy improvement
theorem apply because for any ![]() :
:
Consider a new environment that is just like the original environment, except with
the requirement that policies be ![]() -soft "moved inside" the environment. The
new environment has the same action and state set as the original and behaves
as follows. If in state
-soft "moved inside" the environment. The
new environment has the same action and state set as the original and behaves
as follows. If in state ![]() and taking action
and taking action ![]() , then with probability
, then with probability
![]() the new environment behaves exactly like the old environment. With
probability
the new environment behaves exactly like the old environment. With
probability
![]() it repicks the action at random, with equal probabilities,
and then behaves like the old environment with the new, random action. The best
one can do in this new environment with general policies is the same as the best
one could do in the original environment with
it repicks the action at random, with equal probabilities,
and then behaves like the old environment with the new, random action. The best
one can do in this new environment with general policies is the same as the best
one could do in the original environment with ![]() -soft policies. Let
-soft policies. Let
![]() and
and ![]() denote the optimal value functions for the new environment. Then a
policy
denote the optimal value functions for the new environment. Then a
policy ![]() is optimal among
is optimal among ![]() -soft policies if and only if
-soft policies if and only if ![]() . From
the definition of
. From
the definition of ![]() we know that it is the unique solution to
we know that it is the unique solution to
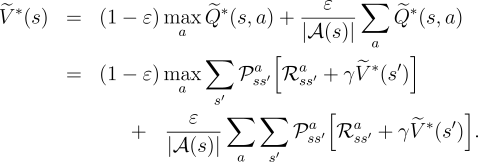
|
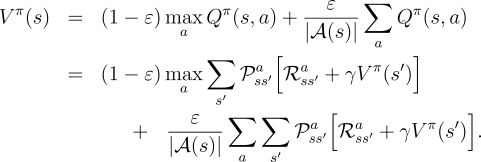
|
In essence, we have shown in the last few pages that policy iteration works for
![]() -soft policies. Using the natural notion of greedy policy for
-soft policies. Using the natural notion of greedy policy for ![]() -soft
policies, one is assured of improvement on every step, except when the best
policy has been found among the
-soft
policies, one is assured of improvement on every step, except when the best
policy has been found among the ![]() -soft policies. This analysis is independent
of how the action-value functions are determined at each stage, but it does
assume that they are computed exactly. This brings us to roughly the
same point as in the previous section. Now we only achieve the best policy
among the
-soft policies. This analysis is independent
of how the action-value functions are determined at each stage, but it does
assume that they are computed exactly. This brings us to roughly the
same point as in the previous section. Now we only achieve the best policy
among the ![]() -soft policies, but on the other hand, we have eliminated the assumption of
exploring starts. The complete algorithm is given in
Figure
5.6.
-soft policies, but on the other hand, we have eliminated the assumption of
exploring starts. The complete algorithm is given in
Figure
5.6.