


Next: 9.8 Summary
Up: 9 Planning and Learning
Previous: 9.6 Trajectory Sampling
The predominant state-space planning methods in artificial intelligence are
collectively known as heuristic search. Although superficially different from
the planning methods we have discussed so far in this chapter, heuristic search and
some of its component ideas can be combined with these methods in useful ways.
Unlike these methods, heuristic search is not concerned with changing the
approximate, or ``heuristic," value function, but only with making improved action
selections given the current value function. In other words, heuristic search is
planning as part of a policy computation.
In heuristic search, for each state encountered, a large
tree of possible continuations is considered. The approximate value function is
applied to the leaf nodes and then backed up toward the current state at the root.
The backing up within the search tree is just the same as in the max-backups (those
for 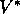 and
and 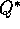 ) discussed throughout this book. The backing up stops at the
state-action nodes for the current state. Once the backed up values of these
nodes are computed, the best of them is chosen as the current action, and then
all backed up values are discarded.
) discussed throughout this book. The backing up stops at the
state-action nodes for the current state. Once the backed up values of these
nodes are computed, the best of them is chosen as the current action, and then
all backed up values are discarded.
In conventional heuristic search no effort is made to save the backed up values by
changing the approximate value function. In fact, the value function is generally
designed by people and never changed as a result of search. However, it is natural
to consider allowing the value function to be improved over time, using either the
backed-up values computed during heuristic search or any of the other methods
presented throughout this book. In a sense we have taken this approach all along.
Our greedy and
 -greedy action-selection methods are not unlike heuristic search, albeit on a
smaller scale. For example, to compute the greedy action given a model
and a state-value function, we must look ahead from each possible action to each
possible next state, backup the rewards and estimated values, and then pick the
best action. Just as in conventional heuristic search, this process computes
backed-up values of the possible actions, but does not attempt to
save them. Thus, heuristic search can be viewed as an extension of the
idea of a greedy policy beyond a single step.
-greedy action-selection methods are not unlike heuristic search, albeit on a
smaller scale. For example, to compute the greedy action given a model
and a state-value function, we must look ahead from each possible action to each
possible next state, backup the rewards and estimated values, and then pick the
best action. Just as in conventional heuristic search, this process computes
backed-up values of the possible actions, but does not attempt to
save them. Thus, heuristic search can be viewed as an extension of the
idea of a greedy policy beyond a single step.
The point of searching deeper than one step is to obtain better action selections.
If one has a
perfect model and an imperfect action-value function, then in fact deeper search
will usually yield better policies. Certainly, if the search
is all the way to the end of the episode, then the effect of the imperfect value
function is eliminated, and the action determined in this way must be optimal. If
the search is of sufficient depth k such that
Certainly, if the search
is all the way to the end of the episode, then the effect of the imperfect value
function is eliminated, and the action determined in this way must be optimal. If
the search is of sufficient depth k such that 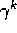 is very small, then the
actions will be correspondingly near optimal. On the other hand, the deeper the
search, the more computation is required, usually resulting in a slower response
time. A good example is provided by Tesauro's grandmaster-level backgammon player,
TD-Gammon (Section 11 .1
). This system used TD(
is very small, then the
actions will be correspondingly near optimal. On the other hand, the deeper the
search, the more computation is required, usually resulting in a slower response
time. A good example is provided by Tesauro's grandmaster-level backgammon player,
TD-Gammon (Section 11 .1
). This system used TD(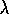 )
to learn an
after-state value function through many games of self-play, using a form
of heuristic search to make its moves. As a model,
TD-Gammon used a priori knowledge of the probabilities of dice rolls and
the assumption that the opponent always selected the actions that TD-Gammon
rated as best for it. Tesauro found that the deeper the heuristic search, the
better the moves made by TD-Gammon, but the longer it took to make each move.
Backgammon has a large branching factor, yet moves must be made within a few
seconds. It was only feasible to search ahead selectively a few steps, but even so
the search resulted in significantly better action selections.
)
to learn an
after-state value function through many games of self-play, using a form
of heuristic search to make its moves. As a model,
TD-Gammon used a priori knowledge of the probabilities of dice rolls and
the assumption that the opponent always selected the actions that TD-Gammon
rated as best for it. Tesauro found that the deeper the heuristic search, the
better the moves made by TD-Gammon, but the longer it took to make each move.
Backgammon has a large branching factor, yet moves must be made within a few
seconds. It was only feasible to search ahead selectively a few steps, but even so
the search resulted in significantly better action selections.
So far we have emphasized heuristic search as an action-selection technique, but
this may not be its most important aspect. Heuristic search also suggests ways of
selectively distributing backups that may lead to better and faster approximation
of the optimal value function. A great deal of research on heuristic search has
been devoted to making the search as efficient as possible. The search tree is
grown very selectively, deeper along some lines and shallower along others. For
example, the search tree is often deeper for the actions that seem most likely to
be best, shallower for those that the agent will probably not want to take anyway.
Can we use a similar idea to improve the distribution of backups? Perhaps it can
be done by preferentially, updating state-action pairs whose values
appears to be close to the maximum available from the state. To our knowledge, this
and other possibilities for distributing backups based on ideas borrowed from
heuristic search have not yet been explored.
We should not overlook the most obvious way in which heuristic search focuses
backups: on the current state. Much of the effectiveness of heuristic search is
due to its search tree being tightly focused on the states and actions that might
immediately follow the current state. You may spend
more of your life playing chess than checkers, but when you play checkers it pays
to think about checkers and about your particular checkers position, your likely
next moves, and successor positions. However you select actions, it is these states
and actions that are of highest priority for backups and where you most urgently
want your approximate value function to be accurate. Not only should your
computation be preferentially devoted to imminent events, but so should your
limited memory resources. In chess, for example, there are far too many possible
positions to store distinct value estimates for each of them, but chess programs
based on heuristic search can easily store distinct estimates for the millions of
positions they encounter looking ahead from a single position. This great focusing
of memory and computational resources on the current decision is presumably the
reason why heuristic search can be so effective.
The distribution of backups can be altered in similar ways to focus on the current
state and its likely successors. As a limiting case we might use exactly the
methods of heuristic search to construct a search tree, and then perform the
individual, 1-step backups from bottom up, as suggested by
Figure 9.15. If the backups are ordered in this way and a
table-lookup representation is used, then
exactly the same backup would be achieved as in heuristic search. Any state-space
search can be viewed in this way as the piecing together of a large number of
individual 1-step backups. Thus, the performance improvement observed with deeper
searches is not due to the use of multi-step backups as such. Instead, it is due to
the focus and concentration of backups on states and actions immediately downstream
from the current state. By devoting a large amount of computation specifically
relevant to the candidate actions, a much better decision can be made than by
relying on unfocused backups.
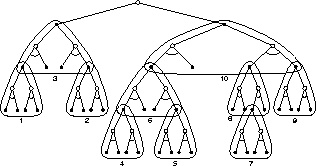
Figure 9.15: The deep backups of heuristic search can be implemented as a sequence of
1-step backups (shown here outlined). The ordering shown is for a selective
depth-first search.



Next: 9.8 Summary
Up: 9 Planning and Learning
Previous: 9.6 Trajectory Sampling
Richard Sutton
Fri May 30 17:11:38 EDT 1997
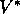 and
and 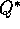 ) discussed throughout this book. The backing up stops at the
state-action nodes for the current state. Once the backed up values of these
nodes are computed, the best of them is chosen as the current action, and then
all backed up values are discarded.
) discussed throughout this book. The backing up stops at the
state-action nodes for the current state. Once the backed up values of these
nodes are computed, the best of them is chosen as the current action, and then
all backed up values are discarded.



 -greedy action-selection methods are not unlike heuristic search, albeit on a
smaller scale. For example, to compute the greedy action given a model
and a state-value function, we must look ahead from each possible action to each
possible next state, backup the rewards and estimated values, and then pick the
best action. Just as in conventional heuristic search, this process computes
backed-up values of the possible actions, but does not attempt to
save them. Thus, heuristic search can be viewed as an extension of the
idea of a greedy policy beyond a single step.
-greedy action-selection methods are not unlike heuristic search, albeit on a
smaller scale. For example, to compute the greedy action given a model
and a state-value function, we must look ahead from each possible action to each
possible next state, backup the rewards and estimated values, and then pick the
best action. Just as in conventional heuristic search, this process computes
backed-up values of the possible actions, but does not attempt to
save them. Thus, heuristic search can be viewed as an extension of the
idea of a greedy policy beyond a single step.

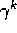 is very small, then the
actions will be correspondingly near optimal. On the other hand, the deeper the
search, the more computation is required, usually resulting in a slower response
time. A good example is provided by Tesauro's grandmaster-level backgammon player,
TD-Gammon (Section 11 .1
). This system used TD(
is very small, then the
actions will be correspondingly near optimal. On the other hand, the deeper the
search, the more computation is required, usually resulting in a slower response
time. A good example is provided by Tesauro's grandmaster-level backgammon player,
TD-Gammon (Section 11 .1
). This system used TD(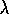 )
to learn an
after-state value function through many games of self-play, using a form
of heuristic search to make its moves. As a model,
TD-Gammon used a priori knowledge of the probabilities of dice rolls and
the assumption that the opponent always selected the actions that TD-Gammon
rated as best for it. Tesauro found that the deeper the heuristic search, the
better the moves made by TD-Gammon, but the longer it took to make each move.
Backgammon has a large branching factor, yet moves must be made within a few
seconds. It was only feasible to search ahead selectively a few steps, but even so
the search resulted in significantly better action selections.
)
to learn an
after-state value function through many games of self-play, using a form
of heuristic search to make its moves. As a model,
TD-Gammon used a priori knowledge of the probabilities of dice rolls and
the assumption that the opponent always selected the actions that TD-Gammon
rated as best for it. Tesauro found that the deeper the heuristic search, the
better the moves made by TD-Gammon, but the longer it took to make each move.
Backgammon has a large branching factor, yet moves must be made within a few
seconds. It was only feasible to search ahead selectively a few steps, but even so
the search resulted in significantly better action selections.
