


Next: 8.2 Gradient-Descent Methods
Up: 8 Generalization and Function
Previous: 8 Generalization and Function
As usual, we begin with the prediction problem, that of estimating the
state-value function 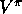 from experience generated using policy
from experience generated using policy  .
The novelty in this chapter is that the approximate value function at time t,
.
The novelty in this chapter is that the approximate value function at time t,
 , is represented not as a table, but as a parameterized functional form with
parameter vector
, is represented not as a table, but as a parameterized functional form with
parameter vector 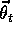 . This means that the
value function
. This means that the
value function 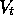 depends totally on
depends totally on 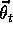 , varying from time step to time
step only as
, varying from time step to time
step only as 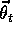 varies. For example,
varies. For example,  might be the function computed
by an artificial neural network, with
might be the function computed
by an artificial neural network, with 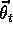 the vector of connection weights.
By adjusting the weights, any of a wide range of different functions
the vector of connection weights.
By adjusting the weights, any of a wide range of different functions 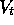 can be
implemented by the network. Or
can be
implemented by the network. Or 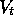 might be the function computed by a decision
tree, where
might be the function computed by a decision
tree, where 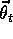 is all the parameters defining the split points and
leaf values of the tree. Typically, the number of parameters (the number of
components of
is all the parameters defining the split points and
leaf values of the tree. Typically, the number of parameters (the number of
components of 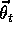 ) is much less than the number of states, and changing one
parameter changes the estimated value of many states. Consequently, when a
single state is backed up, the change generalizes from that state to affect the
values of many other states.
) is much less than the number of states, and changing one
parameter changes the estimated value of many states. Consequently, when a
single state is backed up, the change generalizes from that state to affect the
values of many other states.
All of the prediction methods covered in this book have been described as backups,
that is, as updates to an estimated value function that shift its value at
particular states toward a ``backed-up value" for that state. Let us refer to an
individual backup by the notation 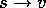 , where s is the state backed up
and v is the backed-up value that s's estimated value is shifted toward. For
example, the DP backup for value prediction is
, where s is the state backed up
and v is the backed-up value that s's estimated value is shifted toward. For
example, the DP backup for value prediction is 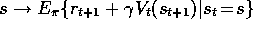 , the Monte Carlo backup is
, the Monte Carlo backup is 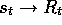 , the TD(0) backup is
, the TD(0) backup is 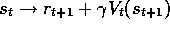 ,
and the general TD(
,
and the general TD(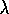 )
backup is
)
backup is 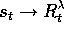 . In the DP
case, an arbitrary state s is backed up, whereas in the the other cases the
state,
. In the DP
case, an arbitrary state s is backed up, whereas in the the other cases the
state, 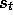 , encountered in (possibly simulated) experience is backed up.
, encountered in (possibly simulated) experience is backed up.
It is natural to interpret each backup as specifying an example of
the desired input-output behavior of the estimated value function. In a
sense, the backup 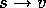 means that the estimated value for state
s should be more like v. Up to now, the actual update implementing the backup
has been trivial: the table entry for s's estimated value has simply been
shifted a fraction of the way towards v. Now we permit arbitrarily complex and
sophisticated function approximation methods to implement the backup. The normal
inputs to these methods are examples of the desired input-output behavior of the
function they are trying to approximate. We use these methods for value
prediction simply by passing to them the
means that the estimated value for state
s should be more like v. Up to now, the actual update implementing the backup
has been trivial: the table entry for s's estimated value has simply been
shifted a fraction of the way towards v. Now we permit arbitrarily complex and
sophisticated function approximation methods to implement the backup. The normal
inputs to these methods are examples of the desired input-output behavior of the
function they are trying to approximate. We use these methods for value
prediction simply by passing to them the 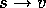 of each
backup as a training example. The approximate function they produce we then
interpret as an estimated value function.
of each
backup as a training example. The approximate function they produce we then
interpret as an estimated value function.
Viewing each backup as a conventional training example in this way enables us to
use any of a wide range of existing function approximation methods for value
prediction. In principle, we can use any method for supervised learning
from examples, including artificial neural networks, decision
trees, and various kinds of multivariate regression. However, not all
function-approximation methods are equally well suited for use in reinforcement
learning. The most sophisticated neural-network and statistical methods all
assume a static training set over which multiple passes are
made. In reinforcement learning, however, it is important that
learning be able to occur online, while interacting with the
environment or with a model of the environment. To do this requires methods
that are able to learn efficiently from incrementally-acquired data.
In addition, reinforcement learning generally requires function approximators
able to handle nonstationary target functions (functions that change over time).
For example, in GPI (Generalized Policy Iteration) control methods we often
seek to learn
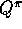 while
while  changes. Even if the policy remains the same, the
target values of training examples are nonstationary if they are generated
by bootstrapping methods (DP and TD). Methods that cannot easily handle
such nonstationarity are less suitable for reinforcement learning.
changes. Even if the policy remains the same, the
target values of training examples are nonstationary if they are generated
by bootstrapping methods (DP and TD). Methods that cannot easily handle
such nonstationarity are less suitable for reinforcement learning.
What performance measures are appropriate for evaluating function-approximation
methods? Most supervised-learning methods seek
to minimize the mean squared error over some distribution, P, of the
inputs. In our value-prediction problem, the inputs are states and the target
function is the true value function 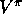 , so the mean squared error (MSE) for
an approximation
, so the mean squared error (MSE) for
an approximation 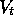 , using parameter
, using parameter 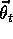 , is
, is

where P is a distribution weighting the errors of different states.
This distribution is important because it is usually not possible to reduce the
error to zero at all states. After all, there are generally far more states than
there are components to 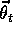 . The flexibility of the function approximator is
thus a scarce resource. Better approximation at some states can be
gained generally only at the expense of worse approximation at other states.
The distribution, P, specifies how these tradeoffs should be made.
. The flexibility of the function approximator is
thus a scarce resource. Better approximation at some states can be
gained generally only at the expense of worse approximation at other states.
The distribution, P, specifies how these tradeoffs should be made.
The distribution P is also usually the
distribution from which the states in the training examples are drawn,
and thus the distribution of states at which backups are done. If we wish to
minimize error over a certain distribution of states, then it makes sense to
train the function approximator with examples from that same distribution. For
example, if you want a uniform level of error over the entire state set, then it
makes sense to train with backups distributed uniformly over the entire state
set, such as in the exhaustive sweeps of some DP methods. Henceforth, let us
assume that the distribution of states at which backups are done and the
distribution that weights errors,
P, are the same.
A distribution of particular interest is the one describing the frequency
with which states are encountered while the agent is
interacting with the environment and selecting actions according to  ,
the policy whose value function we are approximating. We call this the
on-policy distribution, in part because it is the distribution of backups
in on-policy control methods. Minimizing error over the on-policy
distribution focuses function-approximation resources on the states that
actually occur while following the policy, ignoring those that never
occur. The on-policy distribution is also the one for which it is easiest
to get training examples using Monte Carlo or TD methods. These methods
generate backups from sample experience using the policy
,
the policy whose value function we are approximating. We call this the
on-policy distribution, in part because it is the distribution of backups
in on-policy control methods. Minimizing error over the on-policy
distribution focuses function-approximation resources on the states that
actually occur while following the policy, ignoring those that never
occur. The on-policy distribution is also the one for which it is easiest
to get training examples using Monte Carlo or TD methods. These methods
generate backups from sample experience using the policy  . Because a
backup is generated for each state encountered in the experience, the
training examples available are naturally distributed according to the
on-policy distribution. Stronger convergence results are available
for the on-policy distribution than for other distributions, as we discuss
later.
. Because a
backup is generated for each state encountered in the experience, the
training examples available are naturally distributed according to the
on-policy distribution. Stronger convergence results are available
for the on-policy distribution than for other distributions, as we discuss
later.
It is not completely clear that we should care about minimizing the MSE. Our
goal in value prediction is potentially different because our ultimate purpose is
to use the predictions to aid in finding a better policy. The best predictions
for that purpose are not necessarily the best for minimizing MSE. However, it is
not yet clear what a more useful alternative goal for value prediction might be.
For now, we continue to focus on MSE.
An ideal goal in terms of MSE would be to find a global optimum, a
parameter vector 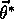 for which
for which 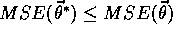 for all possible
for all possible
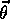 . Reaching this goal is sometimes possible for simple function
approximators such as linear ones, but is rarely possible for complex function
approximators such as artificial neural networks and decision trees. Short of
this, complex function approximators may seek to converge instead to a local
optimum, a parameter
. Reaching this goal is sometimes possible for simple function
approximators such as linear ones, but is rarely possible for complex function
approximators such as artificial neural networks and decision trees. Short of
this, complex function approximators may seek to converge instead to a local
optimum, a parameter
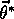 for which
for which
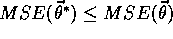 for all
for all 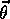 in some neighborhood of
in some neighborhood of  .
Although this guarantee is only slightly reassuring, it is typically the best
that can be said for nonlinear function approximators. For many cases of
interest in reinforcement learning, convergence to an optimum, or even true
convergence, does not occur. Nevertheless, a MSE that is within a small bound
of an optimum may still be achieved with some methods. Others may in fact
diverge, with their MSE approaching infinity in the limit.
.
Although this guarantee is only slightly reassuring, it is typically the best
that can be said for nonlinear function approximators. For many cases of
interest in reinforcement learning, convergence to an optimum, or even true
convergence, does not occur. Nevertheless, a MSE that is within a small bound
of an optimum may still be achieved with some methods. Others may in fact
diverge, with their MSE approaching infinity in the limit.
In this section we have outlined a framework for combining a wide range of
reinforcement learning methods for value prediction with a wide range of
function-approximation methods, using the backups of the former to generate
training examples for the latter. We have also outlined a range of MSE
performance measures to which these methods may aspire. The range of possible
methods is far too large to cover all, and anyway there is too little known
about most of them to make a reliable evaluation or recommendation. Of
necessity, we consider only a few possibilities. In the rest of this
chapter we focus on function-approximation methods based on gradient
principles, and on linear gradient-descent methods in particular. We focus
of these methods in part because we consider them to be particularly
promising and because they reveal key theoretical issues, but also just
because they are simple and our space is limited. If we had another chapter
devoted to function approximation, we would also cover at least memory-based
methods and decision-tree methods.



Next: 8.2 Gradient-Descent Methods
Up: 8 Generalization and Function
Previous: 8 Generalization and Function
Richard Sutton
Sat May 31 15:08:20 EDT 1997
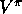 from experience generated using policy
from experience generated using policy  .
The novelty in this chapter is that the approximate value function at time t,
.
The novelty in this chapter is that the approximate value function at time t,
 , is represented not as a table, but as a parameterized functional form with
parameter vector
, is represented not as a table, but as a parameterized functional form with
parameter vector 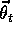 . This means that the
value function
. This means that the
value function 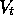 depends totally on
depends totally on 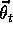 , varying from time step to time
step only as
, varying from time step to time
step only as 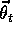 varies. For example,
varies. For example,  might be the function computed
by an artificial neural network, with
might be the function computed
by an artificial neural network, with 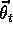 the vector of connection weights.
By adjusting the weights, any of a wide range of different functions
the vector of connection weights.
By adjusting the weights, any of a wide range of different functions 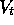 can be
implemented by the network. Or
can be
implemented by the network. Or 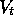 might be the function computed by a decision
tree, where
might be the function computed by a decision
tree, where 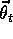 is all the parameters defining the split points and
leaf values of the tree. Typically, the number of parameters (the number of
components of
is all the parameters defining the split points and
leaf values of the tree. Typically, the number of parameters (the number of
components of 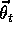 ) is much less than the number of states, and changing one
parameter changes the estimated value of many states. Consequently, when a
single state is backed up, the change generalizes from that state to affect the
values of many other states.
) is much less than the number of states, and changing one
parameter changes the estimated value of many states. Consequently, when a
single state is backed up, the change generalizes from that state to affect the
values of many other states.



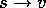 , where s is the state backed up
and v is the backed-up value that s's estimated value is shifted toward. For
example, the DP backup for value prediction is
, where s is the state backed up
and v is the backed-up value that s's estimated value is shifted toward. For
example, the DP backup for value prediction is 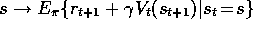 , the Monte Carlo backup is
, the Monte Carlo backup is 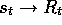 , the TD(0) backup is
, the TD(0) backup is 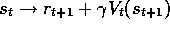 ,
and the general TD(
,
and the general TD(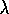 )
backup is
)
backup is 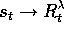 . In the DP
case, an arbitrary state s is backed up, whereas in the the other cases the
state,
. In the DP
case, an arbitrary state s is backed up, whereas in the the other cases the
state, 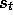 , encountered in (possibly simulated) experience is backed up.
, encountered in (possibly simulated) experience is backed up.
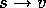 means that the estimated value for state
s should be more like v. Up to now, the actual update implementing the backup
has been trivial: the table entry for s's estimated value has simply been
shifted a fraction of the way towards v. Now we permit arbitrarily complex and
sophisticated function approximation methods to implement the backup. The normal
inputs to these methods are examples of the desired input-output behavior of the
function they are trying to approximate. We use these methods for value
prediction simply by passing to them the
means that the estimated value for state
s should be more like v. Up to now, the actual update implementing the backup
has been trivial: the table entry for s's estimated value has simply been
shifted a fraction of the way towards v. Now we permit arbitrarily complex and
sophisticated function approximation methods to implement the backup. The normal
inputs to these methods are examples of the desired input-output behavior of the
function they are trying to approximate. We use these methods for value
prediction simply by passing to them the 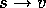 of each
backup as a training example. The approximate function they produce we then
interpret as an estimated value function.
of each
backup as a training example. The approximate function they produce we then
interpret as an estimated value function.
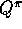 while
while  changes. Even if the policy remains the same, the
target values of training examples are nonstationary if they are generated
by bootstrapping methods (DP and TD). Methods that cannot easily handle
such nonstationarity are less suitable for reinforcement learning.
changes. Even if the policy remains the same, the
target values of training examples are nonstationary if they are generated
by bootstrapping methods (DP and TD). Methods that cannot easily handle
such nonstationarity are less suitable for reinforcement learning.
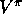 , so the mean squared error (MSE) for
an approximation
, so the mean squared error (MSE) for
an approximation 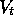 , using parameter
, using parameter 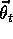 , is
, is

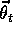 . The flexibility of the function approximator is
thus a scarce resource. Better approximation at some states can be
gained generally only at the expense of worse approximation at other states.
The distribution, P, specifies how these tradeoffs should be made.
. The flexibility of the function approximator is
thus a scarce resource. Better approximation at some states can be
gained generally only at the expense of worse approximation at other states.
The distribution, P, specifies how these tradeoffs should be made.
 ,
the policy whose value function we are approximating. We call this the
on-policy distribution, in part because it is the distribution of backups
in on-policy control methods. Minimizing error over the on-policy
distribution focuses function-approximation resources on the states that
actually occur while following the policy, ignoring those that never
occur. The on-policy distribution is also the one for which it is easiest
to get training examples using Monte Carlo or TD methods. These methods
generate backups from sample experience using the policy
,
the policy whose value function we are approximating. We call this the
on-policy distribution, in part because it is the distribution of backups
in on-policy control methods. Minimizing error over the on-policy
distribution focuses function-approximation resources on the states that
actually occur while following the policy, ignoring those that never
occur. The on-policy distribution is also the one for which it is easiest
to get training examples using Monte Carlo or TD methods. These methods
generate backups from sample experience using the policy  . Because a
backup is generated for each state encountered in the experience, the
training examples available are naturally distributed according to the
on-policy distribution. Stronger convergence results are available
for the on-policy distribution than for other distributions, as we discuss
later.
. Because a
backup is generated for each state encountered in the experience, the
training examples available are naturally distributed according to the
on-policy distribution. Stronger convergence results are available
for the on-policy distribution than for other distributions, as we discuss
later.
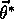 for which
for which 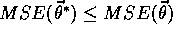 for all possible
for all possible
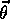 . Reaching this goal is sometimes possible for simple function
approximators such as linear ones, but is rarely possible for complex function
approximators such as artificial neural networks and decision trees. Short of
this, complex function approximators may seek to converge instead to a local
optimum, a parameter
. Reaching this goal is sometimes possible for simple function
approximators such as linear ones, but is rarely possible for complex function
approximators such as artificial neural networks and decision trees. Short of
this, complex function approximators may seek to converge instead to a local
optimum, a parameter
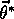 for which
for which
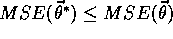 for all
for all 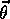 in some neighborhood of
in some neighborhood of  .
Although this guarantee is only slightly reassuring, it is typically the best
that can be said for nonlinear function approximators. For many cases of
interest in reinforcement learning, convergence to an optimum, or even true
convergence, does not occur. Nevertheless, a MSE that is within a small bound
of an optimum may still be achieved with some methods. Others may in fact
diverge, with their MSE approaching infinity in the limit.
.
Although this guarantee is only slightly reassuring, it is typically the best
that can be said for nonlinear function approximators. For many cases of
interest in reinforcement learning, convergence to an optimum, or even true
convergence, does not occur. Nevertheless, a MSE that is within a small bound
of an optimum may still be achieved with some methods. Others may in fact
diverge, with their MSE approaching infinity in the limit.