


Next: 7.5 Sarsa()
Up: 7 Eligibility Traces
Previous: 7.3 The Backward View
In this section we show that offline TD(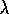 )
, as defined
mechanistically above, achieves the same weight updates as the offline
)
, as defined
mechanistically above, achieves the same weight updates as the offline 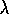 -return
algorithm. In this sense we align the forward (theoretical) and
backward (mechanistic) views of
TD(
-return
algorithm. In this sense we align the forward (theoretical) and
backward (mechanistic) views of
TD(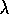 )
. Let
)
. Let 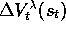 denote the update at time t of
denote the update at time t of 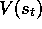 according to the
according to the
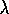 -return algorithm (7.4), and let
-return algorithm (7.4), and let 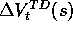 denote the update
at time t of state s according to the mechanistic definition of TD(
denote the update
at time t of state s according to the mechanistic definition of TD(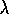 )
as
given by (7.7). Then our goal is to
show that, over an episode, the sum of all the updates is the same for the two
algorithms:
)
as
given by (7.7). Then our goal is to
show that, over an episode, the sum of all the updates is the same for the two
algorithms:
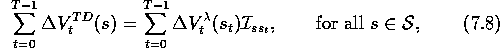
where 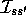 is an identity-indicator function, equal to 1 if
is an identity-indicator function, equal to 1 if 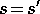 and equal to 0 otherwise.
and equal to 0 otherwise.
First note that an accumulating eligibility trace can be written
explicitly (non-recursively) as
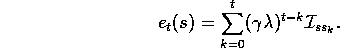
Thus, the lefthand side of (7.8) can be written
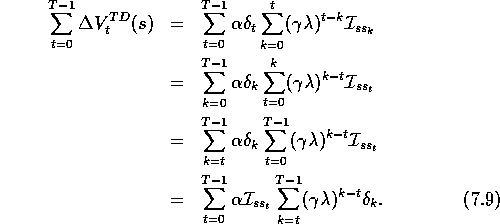
Now we turn to the righthand side of (7.8).
Consider an individual update of the  -return algorithm:
-return algorithm:
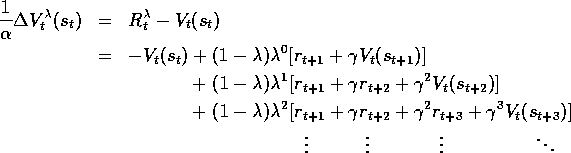
Examine the first column inside the brackets---all the  's with
their weighting factors of
's with
their weighting factors of 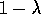 times powers of
times powers of 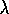 . It turns out that all the
weighting factors sum to 1. Thus we can pull out the first column and get just
an unweighted term of
. It turns out that all the
weighting factors sum to 1. Thus we can pull out the first column and get just
an unweighted term of 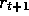 . A similar trick pulls out the second column in
brackets, starting from the second row, which sums to
. A similar trick pulls out the second column in
brackets, starting from the second row, which sums to 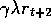 . Repeating
this for each column, we get
. Repeating
this for each column, we get
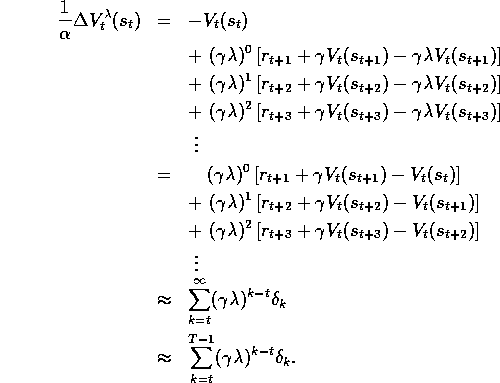
The approximation above is exact in the case of offline updating, in which case
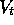 is the same for all t. The last step is exact (not an approximation)
because all the
is the same for all t. The last step is exact (not an approximation)
because all the
 terms omitted are due to fictitious steps ``after" the terminal state has been
entered. All these steps have zero rewards and zero values; thus all their
terms omitted are due to fictitious steps ``after" the terminal state has been
entered. All these steps have zero rewards and zero values; thus all their
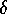 's are zero as well. Thus, we have shown that in the offline case the
righthand side of (7.8) can be written
's are zero as well. Thus, we have shown that in the offline case the
righthand side of (7.8) can be written
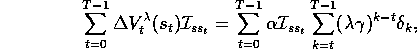
which is the same as (7.9). This proves (7.8).
In the case of online updating, the approximation made above will be close as
long as 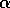 is small and thus
is small and thus 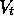 changes little during an episode. Even in
the online case we can expect the updates of TD(
changes little during an episode. Even in
the online case we can expect the updates of TD(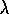 )
and of the
)
and of the 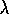 -return algorithm
to be similar.
-return algorithm
to be similar.
For the moment let us assume that the increments are small
enough during an episode that online TD(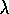 )
gives essentially the same update over
the course of an episode as does the
)
gives essentially the same update over
the course of an episode as does the 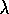 -return algorithm. There still remain
interesting questions about what happens during an episode. Consider the
updating of the value of state
-return algorithm. There still remain
interesting questions about what happens during an episode. Consider the
updating of the value of state 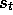 in mid-episode, at time t+k. Under online
TD(
in mid-episode, at time t+k. Under online
TD(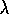 )
, the effect at t+k is just as if we had done a
)
, the effect at t+k is just as if we had done a 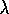 -return update treating
the last observed state as the terminal state of the episode with a nonzero
terminal value equal to its current estimated value. This relationship is
maintained from step to step as each new state is observed.
-return update treating
the last observed state as the terminal state of the episode with a nonzero
terminal value equal to its current estimated value. This relationship is
maintained from step to step as each new state is observed.
Example  .
.
Random Walk with TD(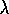 )
.
Because offline TD(
)
.
Because offline TD(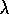 )
is equivalent to the
)
is equivalent to the 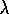 -return algorithm, we already have
the results for offline TD(
-return algorithm, we already have
the results for offline TD(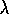 )
on the 19-state random walk task; they are shown
in Figure 7.6. The comparable results for online TD(
)
on the 19-state random walk task; they are shown
in Figure 7.6. The comparable results for online TD(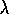 )
are
shown in Figure 7.9. Note that the online algorithm works
better over a broader range of parameters. This is often found to be the case for
online methods.
)
are
shown in Figure 7.9. Note that the online algorithm works
better over a broader range of parameters. This is often found to be the case for
online methods.
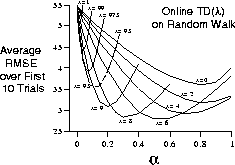
Figure 7.9: Performance of online TD( )
on the 19-state random-walk task.
)
on the 19-state random-walk task.
Exercise  .
.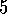
As we have noted, when done online, TD(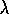 )
only approximates the
)
only approximates the 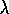 -return
algorithm. We sometimes wonder if there isn't some slightly different TD method
which would maintain the equivalence even in the online case. One idea is to
define the TD error instead as
-return
algorithm. We sometimes wonder if there isn't some slightly different TD method
which would maintain the equivalence even in the online case. One idea is to
define the TD error instead as
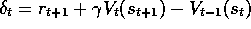 . Show that in this case the
modified TD(
. Show that in this case the
modified TD(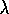 )
algorithm would then achieve exactly
)
algorithm would then achieve exactly
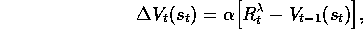
even in the case of online updating with large 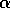 . Would this alternate
TD(
. Would this alternate
TD(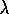 )
be better or worse than the one described in the text? Describe an
experiment or analysis that would help answer this question.
)
be better or worse than the one described in the text? Describe an
experiment or analysis that would help answer this question.



Next: 7.5 Sarsa()
Up: 7 Eligibility Traces
Previous: 7.3 The Backward View
Richard Sutton
Fri May 30 15:01:47 EDT 1997
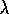 )
, as defined
mechanistically above, achieves the same weight updates as the offline
)
, as defined
mechanistically above, achieves the same weight updates as the offline 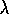 -return
algorithm. In this sense we align the forward (theoretical) and
backward (mechanistic) views of
TD(
-return
algorithm. In this sense we align the forward (theoretical) and
backward (mechanistic) views of
TD(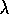 )
. Let
)
. Let 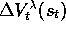 denote the update at time t of
denote the update at time t of 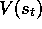 according to the
according to the
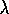 -return algorithm (7.4), and let
-return algorithm (7.4), and let 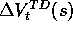 denote the update
at time t of state s according to the mechanistic definition of TD(
denote the update
at time t of state s according to the mechanistic definition of TD(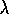 )
as
given by (7.7). Then our goal is to
show that, over an episode, the sum of all the updates is the same for the two
algorithms:
)
as
given by (7.7). Then our goal is to
show that, over an episode, the sum of all the updates is the same for the two
algorithms:



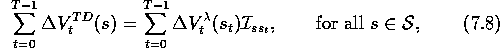
 is an identity-indicator function, equal to 1 if
is an identity-indicator function, equal to 1 if  and equal to 0 otherwise.
and equal to 0 otherwise.
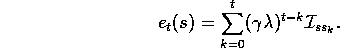
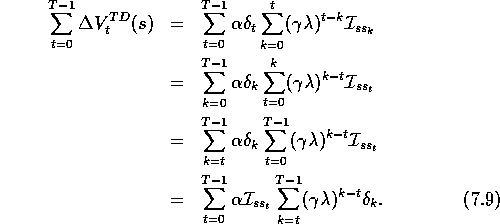
 -return algorithm:
-return algorithm:
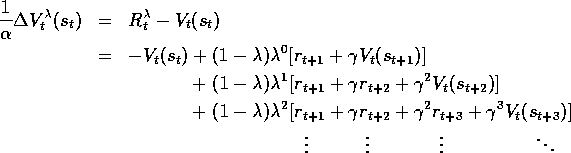
 's with
their weighting factors of
's with
their weighting factors of 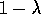 times powers of
times powers of 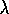 . It turns out that all the
weighting factors sum to 1. Thus we can pull out the first column and get just
an unweighted term of
. It turns out that all the
weighting factors sum to 1. Thus we can pull out the first column and get just
an unweighted term of 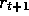 . A similar trick pulls out the second column in
brackets, starting from the second row, which sums to
. A similar trick pulls out the second column in
brackets, starting from the second row, which sums to 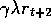 . Repeating
this for each column, we get
. Repeating
this for each column, we get
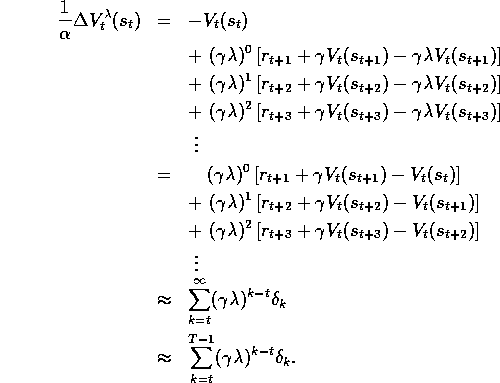
 is the same for all t. The last step is exact (not an approximation)
because all the
is the same for all t. The last step is exact (not an approximation)
because all the
 terms omitted are due to fictitious steps ``after" the terminal state has been
entered. All these steps have zero rewards and zero values; thus all their
terms omitted are due to fictitious steps ``after" the terminal state has been
entered. All these steps have zero rewards and zero values; thus all their
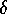 's are zero as well. Thus, we have shown that in the offline case the
righthand side of (
's are zero as well. Thus, we have shown that in the offline case the
righthand side of (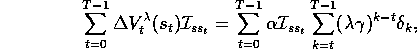
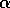 is small and thus
is small and thus 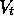 changes little during an episode. Even in
the online case we can expect the updates of TD(
changes little during an episode. Even in
the online case we can expect the updates of TD(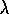 )
and of the
)
and of the 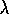 -return algorithm
to be similar.
-return algorithm
to be similar.
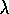 )
gives essentially the same update over
the course of an episode as does the
)
gives essentially the same update over
the course of an episode as does the 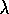 -return algorithm. There still remain
interesting questions about what happens during an episode. Consider the
updating of the value of state
-return algorithm. There still remain
interesting questions about what happens during an episode. Consider the
updating of the value of state 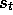 in mid-episode, at time t+k. Under online
TD(
in mid-episode, at time t+k. Under online
TD(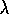 )
, the effect at t+k is just as if we had done a
)
, the effect at t+k is just as if we had done a 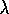 -return update treating
the last observed state as the terminal state of the episode with a nonzero
terminal value equal to its current estimated value. This relationship is
maintained from step to step as each new state is observed.
-return update treating
the last observed state as the terminal state of the episode with a nonzero
terminal value equal to its current estimated value. This relationship is
maintained from step to step as each new state is observed.
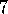 .
.
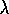 )
.
Because offline TD(
)
.
Because offline TD(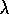 )
is equivalent to the
)
is equivalent to the 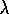 -return algorithm, we already have
the results for offline TD(
-return algorithm, we already have
the results for offline TD(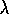 )
on the 19-state random walk task; they are shown
in Figure
)
on the 19-state random walk task; they are shown
in Figure 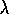 )
are
shown in Figure
)
are
shown in Figure 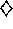

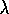 )
on the 19-state random-walk task.
)
on the 19-state random-walk task.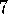 .
.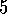
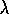 )
only approximates the
)
only approximates the 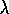 -return
algorithm. We sometimes wonder if there isn't some slightly different TD method
which would maintain the equivalence even in the online case. One idea is to
define the TD error instead as
-return
algorithm. We sometimes wonder if there isn't some slightly different TD method
which would maintain the equivalence even in the online case. One idea is to
define the TD error instead as
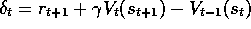 . Show that in this case the
modified TD(
. Show that in this case the
modified TD(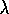 )
algorithm would then achieve exactly
)
algorithm would then achieve exactly
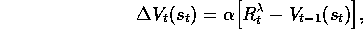
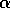 . Would this alternate
TD(
. Would this alternate
TD(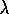 )
be better or worse than the one described in the text? Describe an
experiment or analysis that would help answer this question.
)
be better or worse than the one described in the text? Describe an
experiment or analysis that would help answer this question.