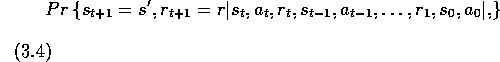



In the reinforcement learning framework, the agent makes its decisions on the basis of a signal from the environment called the environment's state. In this section we discuss what is required of the state signal, and what kind of information we should and should not expect it to provide. In particular, we formally define a property of environment's and their state signals that is of particular interest, called the Markov property.
In this book, by the state we mean just whatever information is available to the agent. We assume that the state is given by some preprocessing system which is nominally part of the environment. We do not address the issues of constructing, changing, or learning the state signal in this book. We take this approach not because we consider state representation to be unimportant, but in order to focus fully on the decision-making issues. In other words, our main concern is not with designing the state signal, but on deciding what action to take as a function of whatever state signal is available.
Certainly the state signal should include immediate sensations such as sensory measurements, but it can contain much more than that. State representations can be highly processed versions of original sensations, or they can be complex structures built up over time from the sequence of sensations. For example, as people we move our eyes over a scene, with only a tiny spot (the fovea) visible in detail at any one time, and yet build up a rich and detailed representation of a scene. Or, more obviously, we can look at an object, then look away, and still know that it is there. We can hear the word ``Yes," and consider ourselves to be in totally different states depending on the question that came before and which is no longer audible. At a more mundane level, a control system can measure position at two different times to produce a state representation including velocity. In all of these cases the state is constructed and maintained based on immediate sensations together with the previous state or some other memory of past sensations. In this book, we do not explore how that is done, but certainly it could be and has been done. There is no reason to restrict the state representation to immediate sensations; in typical applications we should expect the state representation to be able to inform the agent of more than that.
On the other hand, the state signal should not be expected to inform the agent of everything about the environment, or even everything that could be useful to it in making decisions. If the agent is playing blackjack, we should not expect it to know what the next card is in the deck. If the agent is answering the phone, we should not expect it to know in advance who the caller is. If the agent is a paramedic called to a road accident, we should not expect it to know immediately the internal injuries of an unconscious victim. In all of these cases there is hidden state information in the environment, and that information would be useful if the agent knew it, but the agent could not know it because it has never received any relevant sensations. In short, we don't fault an agent for not knowing something that matters, but only for having known something and then forgotten it!
What we would like, ideally, is a state signal that summarizes past sensations compactly yet in such a way that all relevant information is retained. This normally requires more than the immediate sensations, but never more than the complete history of all past sensations. A state signal that succeeds in retaining all relevant information is said to be Markov, or to have the Markov property (we define this formally below). For example, a checkers position---the current configuration of all the pieces on the board---would serve as a Markov state because it summarizes everything important about the complete sequence of positions that led to it. Much of the information about the sequence is lost, but all that really matters for the future of the game is retained. Similarly, the current position and velocity of a cannon ball is all that matters for its future flight. It doesn't matter how that position and velocity came about. This is sometimes also referred to as an ``independence of path" property because all that matters is in the current state signal; its meaning is independent of the ``path," or history, of signals that have led up to it.
We now formally define the Markov property for the reinforcement learning problem. To keep the mathematics simple, we assume here that their are a finite number of states and reward values. This enables us to work in terms of sums and probabilities rather than integrals and probability densities, but the argument could easily be extended to include continuous states and rewards. Consider how a general environment might respond at time t+1 to the action taken at time t. In the most general, causal case this response may depend on everything that has happened earlier. In this case the dynamics can be defined only by specifying the complete probability distribution:
for all  , r, and all possible values of the past events:
, r, and all possible values of the past events:
 . If the state signal has the
Markov property, on the other hand, then the environment's response at
t+1 depends only on the state and action representations at t, in which case the
environment's dynamics can be defined by specifying only
. If the state signal has the
Markov property, on the other hand, then the environment's response at
t+1 depends only on the state and action representations at t, in which case the
environment's dynamics can be defined by specifying only
for all  , r,
, r,  , and
, and  . In other words, a state representation
has the Markov property, and is a Markov state, if and only if
(3.5) is equal to (3.4) for all
. In other words, a state representation
has the Markov property, and is a Markov state, if and only if
(3.5) is equal to (3.4) for all
 , r, and histories,
, r, and histories,  .
.
If an environment has the Markov property, then its one-step dynamics (3.5) enable us to predict the next state and expected next reward given the current state and action. One can show that by iterating this equation one can predict all future states and expected rewards from knowledge only of the current state as well as is possible given the complete history up to the current time. It also follows that Markov states provide the best possible basis for choosing actions. That is, the best policy for choosing actions as a function of a Markov state signal is just as good as the best policy for choosing actions as a function of complete histories.
Even when the state signal is non-Markov, it is still appropriate to think of the state in reinforcement learning as an approximation to a Markov state. In particular, we always want the state to be a good basis for predicting future rewards and for selecting actions. In cases in which a model of the environment is learned (see Chapter 9), we also want the state to be a good basis for predicting subsequent states. Markov states provide an unsurpassed basis for doing all of these things. To the extent that the state approaches the ability of Markov states in these ways, one will obtain better performance from reinforcement learning systems. For all of these reasons, it is useful to think of the state at each time step as an approximation to a Markov state, although one should remember that it may not fully satisfy the Markov property.
The Markov property is important in reinforcement learning because decisions and values are assumed to be a function only of the current state. In order for these to be effective and informative, the state representation must be informative. All of the theory presented in this book assumes Markov state signals. This means that not all the theory strictly applies to cases in which the Markov property does not strictly apply. However, the theory developed for the Markov case still helps us to understand the behavior of the algorithms, and the algorithm can and have been successfully applied to many tasks that were not strictly Markov. A full understanding of the theory of the Markov case is an essential foundation for extending it to the more complex and realistic non-Markov case. Finally, we note that the assumption of Markov state representations is not unique to reinforcement learning, but is also present in most if not all other approaches to artificial intelligence.
Example  .
.
Pole-Balancing State. In the pole-balancing task introduced earlier, a state signal would be Markov if it exactly specified, or made it possible to exactly reconstruct, the position and velocity of the cart along the track, the angle between the cart and the pole, and the rate at which this angle is changing (the angular velocity). In an idealized cart-pole system, this information would be sufficient to exactly predict the future behavior of the cart and pole, given the actions taken by the controller. In practice, however, it is never possible to know this information exactly because any real sensor would introduce some distortion and delay in its measurements. Furthermore, in any real cart-pole system there are always other effects, such as the bending of the pole, the temperatures of the wheel and pole bearings, and various forms of backlash, which slightly affect the behavior of the system. These factors would cause violations of the Markov property if the state signal were only the positions and velocities of the cart and the pole.
However, often the positions and velocities serve quite well as states.
Some early studies of learning to solve the pole-balancing task used a very
coarse state signal which divided cart positions into three regions:
right, left, and middle (and similar rough quantizations of the
other three intrinsic state variables). This distinctly non-Markov state was
sufficient to allow the task to be solved easily by reinforcement learning
methods. In fact, this coarse representation may have facilitated rapid learning
by forcing the learning agent to ignore fine distinctions that would not have
been useful in solving the task.

Example  .
.
Draw Poker. In draw poker, each player is dealt a hand of five cards. There is a round of betting, in which each player exchanges some of his cards for new ones, and then there is a final round of betting. At each round of betting, each player must match the highest bets of the other players or else drop out (fold). After the second round of betting, the player with the best hand who has not folded is the winner and collects all the bets.
The state signal in draw poker is different for each player. Each player knows the cards in his own hand, but can only guess at those in the other players' hands. A common mistake is to think that a Markov state signal should include the contents of all the players' hands and the cards remaining in the deck. In a fair game, however, we assume that the players are in principle unable to determine these things from their past observations. If a player did know them, then she could predict some future events (such as the cards one could exchange for) better than by remembering all past observations.
In addition to knowledge of one's own cards, the state in draw poker should include the bets and the numbers of cards drawn by the other players. For example, if one of the other players drew three new cards, you may suspect he retained a pair and adjust your guess at the strength of his hand accordingly. The players' bets also influence your assessment of their hands. In fact, much of your past history with these particular players is part of the Markov state. Does Ellen like to bluff, or does she play conservatively? Does her face or demeanor provide clues to the strength of her hand? How does Joe's play change when it is late at night, or when he has already won a lot of money?
Although everything ever observed about the other players may
have an effect on the probabilities that they are holding various kinds of hands,
in practice this is far too much to remember and analyze, and most of it will have
no clear effect on one's predictions and decisions. Very good poker
players are adept at remembering just the key clues, and at sizing up new players
quickly, but no one remembers everything that is relevant. As a result, the
state representations people use to make their poker decisions are undoubtedly
sub-Markov, and the decisions themselves are presumably imperfect. Nevertheless,
people still make very good decisions in such tasks. We conclude that the
inability to have access to a perfect Markov state representation is
probably not a severe problem for a reinforcement learning agent.

Exercise  .
.
Broken Vision System. Imagine that you are a vision system. When you are first turned on for the day, an image floods into your camera. You can see lots of things, but not all things. You can't see objects that are occluded, and of course you can't see objects that are behind you. After seeing that first scene, do you have access to the Markov state of the environment? Suppose your camera was broken that day and you received no images at all, all day. Would you have access to the Markov state then?


