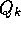The averaging methods discussed so far are appropriate in a
stationary environment, but not if the bandit is changing over time. As we noted
earlier, we often encounter reinforcement learning problems that are
effectively nonstationary. In such cases it makes sense to weight recent
rewards more heavily than long past ones. One of the most popular ways of doing
this is to use a fixed step size. For example, the incremental update
rule (2.4) for updating an average
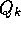of the k past rewards is modified to be
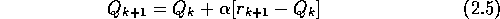
where the step size, 
, 
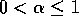, is constant. This
results in
being a weighted average of past rewards and the initial estimate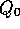 
:
We call this a weighted average because the sum of the weights is 
, as you can check yourself. Note
that the weight, 
, given to the reward, 
,
depends on how many rewards ago, k-i, it was observed. The quantity
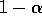is less than 1, and thus the weight given to 
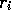decreases as the
number of intervening rewards increases. In fact, the weight decays exponentially
according to the exponent on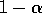 
. Accordingly, this is sometimes called an
exponential, recency-weighted average.
Sometimes it is convenient to vary the step size from step to
step. Let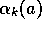 
denote the step size used to process the
reward received after the kth selection of action a. As we have noted, the
choice 
results in the sample-average method, which is guaranteed to
converge to the true action values by the law of large numbers. But of
course convergence is not guaranteed for all choices of the sequence
. A classic result in stochastic approximation theory gives us
the conditions required to assure convergence with probability one:
The first condition is required to guarantee that the steps are large enough to eventually overcome any initial conditions or random fluctuations. The second condition guarantees that eventually the steps become small enough to assure convergence.
Note that both convergence conditions are met for the sample-average case,
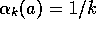, but not for the case of constant step size, 
.
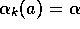In the latter case, the second condition is not met, indicating that the estimates
never completely converge but continue to vary in response to the most
recently received rewards. As we mentioned above, this is actually desirable
in a nonstationary environment, and problems that are effectively nonstationary are
the norm in reinforcement learning. In addition, step-size sequences that meet the
conditions (2.7) often converge very slowly or need
considerable tuning in order to obtain a satisfactory convergence rate. Although
step-size sequences that meet these convergence conditions are often used in
theoretical work, they are seldom used in applications and empirical research.
Exercise 
.
If the step sizes,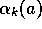 
, are not constant, then the
estimate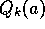 
is a weighted average of previously received rewards
with a weighting different from that given by (2.6). What is
the weighting on each prior reward for the general case?
Exercise 
.
(programming)
Design and conduct an experiment to demonstrate the difficulties that
sample-average methods have on nonstationary problems. Use a
modified version of the 10-armed testbed in which all the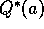 
start out equal
and then take independent random walks. Prepare plots like
Figure 2.1 for an action-value method using sample
averages, incrementally computed by 
, and another action-value method using a
constant step size, 
. Use 
and, if necessary, runs longer than 1000
plays.
