


Next: 7.10 Variable (*)
Up: 7 Eligibility Traces
Previous: 7.8 Replacing Traces
It might at first appear that methods using eligibility traces are much more complex
than 1-step methods. A naive implementation would require every state
(or state-action pair) to update both its value estimate and its eligibility trace
on every time step. This would not be a problem for implementations on
common Single-Instruction-Multiple-Data parallel computers or in plausible neural
implementations, but it is for implementations on conventional serial computers.
Fortunately, for typical values of 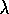 and
and 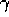 the eligibility traces of almost all
states are always very near zero; only those that have recently been visited will
have traces significantly greater than zero. Only these few states really need to
be updated because the updates at the others will have essentially no effect.
the eligibility traces of almost all
states are always very near zero; only those that have recently been visited will
have traces significantly greater than zero. Only these few states really need to
be updated because the updates at the others will have essentially no effect.
In practice,
then, implementations on conventional computers keep track of and update only the
few states with non-zero traces. Using this trick, the computational expense of
using traces is typically a few times that of a 1-step method. The exact multiple
of course depends on 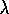 and
and 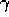 and on the expense of the other computations.
Cichosz (1995) has demonstrated a further implementation
technique which reduces complexity to a constant independent of
and on the expense of the other computations.
Cichosz (1995) has demonstrated a further implementation
technique which reduces complexity to a constant independent of 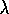 and
and 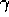 .
Finally, it should be noted that the tabular case is in some sense a worst
case for the computational complexity of traces. When function approximators
are used (Chapter 8
) the computational advantages of not using traces
generally decrease. For example, if artificial neural networks and
backpropagation are used, then traces generally cause only a doubling of the
required memory and computation per step.
.
Finally, it should be noted that the tabular case is in some sense a worst
case for the computational complexity of traces. When function approximators
are used (Chapter 8
) the computational advantages of not using traces
generally decrease. For example, if artificial neural networks and
backpropagation are used, then traces generally cause only a doubling of the
required memory and computation per step.
Exercise 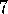 .
.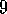
Write pseudocode for an implementation of TD(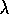 )
that updates only value estimates
for states whose traces are greater than
)
that updates only value estimates
for states whose traces are greater than  .
.
Richard Sutton
Fri May 30 15:01:47 EDT 1997
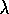 and
and 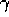 the eligibility traces of almost all
states are always very near zero; only those that have recently been visited will
have traces significantly greater than zero. Only these few states really need to
be updated because the updates at the others will have essentially no effect.
the eligibility traces of almost all
states are always very near zero; only those that have recently been visited will
have traces significantly greater than zero. Only these few states really need to
be updated because the updates at the others will have essentially no effect.



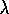 and
and 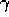 and on the expense of the other computations.
Cichosz (1995) has demonstrated a further implementation
technique which reduces complexity to a constant independent of
and on the expense of the other computations.
Cichosz (1995) has demonstrated a further implementation
technique which reduces complexity to a constant independent of 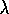 and
and 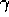 .
Finally, it should be noted that the tabular case is in some sense a worst
case for the computational complexity of traces. When function approximators
are used (Chapter 8
) the computational advantages of not using traces
generally decrease. For example, if artificial neural networks and
backpropagation are used, then traces generally cause only a doubling of the
required memory and computation per step.
.
Finally, it should be noted that the tabular case is in some sense a worst
case for the computational complexity of traces. When function approximators
are used (Chapter 8
) the computational advantages of not using traces
generally decrease. For example, if artificial neural networks and
backpropagation are used, then traces generally cause only a doubling of the
required memory and computation per step.
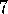 .
.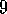
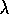 )
that updates only value estimates
for states whose traces are greater than
)
that updates only value estimates
for states whose traces are greater than  .
.