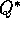 . To achieve this, we first consider
another policy evaluation problem.
. To achieve this, we first consider
another policy evaluation problem.



If a model is not available, then it is particularly useful to estimate
action values rather than state values. With a model, state values
alone are sufficient to determine a policy; one simply looks
ahead one step and chooses whichever action leads to the best combination
of reward and next state, as we did in the chapter on DP.
Without a model, however, state values alone are not sufficient. One must
explicitly estimate the value of each action in order for the values to be
useful in suggesting a policy. Thus, one of our primary goals for Monte
Carlo methods is to estimate 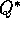 . To achieve this, we first consider
another policy evaluation problem.
. To achieve this, we first consider
another policy evaluation problem.
The policy evaluation problem for action values is to estimate 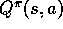 , the
expected return when starting in state s, taking action a, and thereafter
following policy
, the
expected return when starting in state s, taking action a, and thereafter
following policy  . The Monte Carlo methods here
are essentially the same as just presented for state values. The every-visit
MC method estimates the value of a state-action pair as the average of the
returns that have followed visits to the state in which the action
was selected. The first-visit MC method averages the returns following the
first time in each episode that the state was visited and the action
was selected. These methods converge quadratically, as before, to the true
expected values as the number of visits to each state-action pair approaches
infinity.
. The Monte Carlo methods here
are essentially the same as just presented for state values. The every-visit
MC method estimates the value of a state-action pair as the average of the
returns that have followed visits to the state in which the action
was selected. The first-visit MC method averages the returns following the
first time in each episode that the state was visited and the action
was selected. These methods converge quadratically, as before, to the true
expected values as the number of visits to each state-action pair approaches
infinity.
The only complication is that many relevant state-action pairs may never be
visited. If  is a deterministic policy, then in following
is a deterministic policy, then in following  one
will observe returns only for one of the actions from each state. With no
returns to average, the Monte Carlo estimates of the other actions will not
improve with experience. This is a serious
problem because the purpose of learning action values is to help in choosing
among the actions available in each state. To compare alternatives we need to
estimate the value of all the actions from each state, not just the
one we currently favor.
one
will observe returns only for one of the actions from each state. With no
returns to average, the Monte Carlo estimates of the other actions will not
improve with experience. This is a serious
problem because the purpose of learning action values is to help in choosing
among the actions available in each state. To compare alternatives we need to
estimate the value of all the actions from each state, not just the
one we currently favor.
This is the general problem of maintaining exploration, as discussed in the context of the n -armed bandit problem in Chapter 2 . For policy evaluation to work for action values, we must assure continual exploration. One way to do this is by specifying that the first step of each episode starts at a state-action pair, and that every such pair has a nonzero probability of being selected as the start. This guarantees that all state-action pairs will be visited an infinite number of times in the limit of an infinite number of episodes. We call this the assumption of exploring starts.
The assumption of exploring starts is sometimes useful, but of course it cannot be relied upon in general, particularly when learning directly from real interactions with an environment. In that case the starting conditions are unlikely to be that helpful. The most common alternative approach to assuring that all state-action pairs are encountered is simply to consider only policies that are stochastic with a nonzero probability of selecting all actions. We discuss two important variants of this approach in later sections. For now we retain the assumption of exploring starts and complete the presentation of a full Monte Carlo control method.
Exercise  .
.
What is the backup diagram for Monte Carlo estimation of 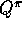 ?
?


