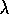1.6 History of Reinforcement Learning

The history of reinforcement learning has two main threads, both long and rich, which were pursued independently before intertwining in modern reinforcement learning. One thread concerns learning by trial and error and started in the psychology of animal learning. This thread runs through some of the earliest work in artificial intelligence and led to the revival of reinforcement learning in the early 1980s. The other thread concerns the problem of optimal control and its solution using value functions and dynamic programming. For the most part, this thread did not involve learning. Although the two threads were largely independent, the exceptions revolve around a third, less distinct thread concerning temporal-difference methods such as used in the Tic-Tac-Toe example in this chapter. All three threads came together in the late 1980s to produce the modern field of reinforcement learning as we present it in this book.

The thread focusing on trial-and-error learning is the one with which we are most familiar and about which we have the most to say in this brief history. Before doing that, however, we briefly discuss the optimal control thread.

The term ``optimal control" came into use in the late 1950s to describe the problem of designing a controller to minimize a measure of a dynamical system's behavior over time. One of the approaches to this problem was developed in the mid-1950s by Richard Bellman and colleagues by extending a 19th century theory of Hamilton and Jacobi. This approach uses the concept of a dynamical system's state and of a value function, or ``optimal return function," to define a functional equation, now often called the Bellman equation. The class of methods for solving optimal control problems by solving this equation came to be known as dynamic programming (Bellman, 1957a). Bellman (1957b) also introduced the discrete stochastic version of the optimal control problem known as Markovian decision processes (MDPs), and

Ron Howard (1960) devised the policy iteration method for MDPs. All of these are essential elements underlying the theory and algorithms of modern reinforcement learning.

Dynamic programming is widely considered the only feasible way of solving general stochastic optimal control problems. It suffers from what Bellman called ``the curse of dimensionality," meaning that its computational requirements grow exponentially with the number of state variables, but it is still far more efficient and more widely applicable than any other method. Dynamic programming has been extensively developed in the last four decades, including extensions to partially observable MDPs (surveyed by Lovejoy, 1991), many applications (surveyed by White, 1985, 1988, 1993), approximation methods (surveyed by Rust, 1996), and asynchronous methods (Bertsekas, 1982, 1983). Many excellent modern treatments of dynamic programming are available (e.g., Bertsekas, 1995; Puterman, 1994; Ross, 1983; and Whittle, 1982, 1983). Bryson (1996) provides a detailed authoritative history of optimal control.

In this book, we consider all of the work on optimal control to also be work in reinforcement learning. We define reinforcement learning as any effective way of solving reinforcement learning problems, and it is now clear that these problems are very closely related to optimal control problems, particularly those formulated as MDPs. Accordingly we must consider the solution methods of optimal control, such as dynamic programming, to also be reinforcement learning methods. Of course, almost all of these methods require complete knowledge of the system to be controlled, and for this reason it feels a little unnatural to say that they are part of reinforcement learning. On the other hand, many dynamic programming methods are incremental and iterative. Like true learning methods, they gradually reach the correct answer through successive approximations. As we show in the rest of this book, these similarities are far more than superficial. The theories and solution methods for the cases of complete and incomplete knowledge are so closely related that we feel they must be considered together as part of the same subject matter.

Let us return now to the other major thread leading to the modern field of reinforcement learning, that centered around the idea of trial-and-error learning. This thread began in psychology, where ``reinforcement" theories of learning are common. Perhaps the first to succintly express the essence of trial-and-error learning was Edward Thorndike. We take this essence to be the idea that actions followed by good or bad outcomes have their tendency to be re-selected altered accordingly. In Thorndike's words:

Of several responses made to the same situation, those which are accompanied or closely followed by satisfaction to the animal will, other things being equal, be more firmly connected with the situation, so that, when it recurs, they will be more likely to recur; those which are accompanied or closely followed by discomfort to the animal will, other things being equal, have their connections with that situation weakened, so that, when it recurs, they will be less likely to occur. The greater the satisfaction or discomfort, the greater the strengthening or weakening of the bond. (Thorndike, 1911, p. 244)

The Law of Effect includes the two most important aspects of what we mean by trial-and-error learning. First, it is selectional rather than instructional in the sense of Monod, meaning that it involves trying alternatives and selecting among them by comparing their consequences. Second, it is associative, meaning that the alternatives found by selection are associated with particular situations. Natural selection in evolution is a prime example of a selectional process, but it is not associative. Supervised learning is associative, but not selectional. It is the combination of these two that is essential to the Law of Effect and to trial-and-error learning. Another way of saying this is that the Law of Effect is an elementary way of combining search and memory: search in the form of trying and selecting among many actions in each situation, and memory in the form of remembering what actions worked best, associating them with the situations in which they were best. Combining search and memory in this way is essential to reinforcement learning.

In early artificial intelligence, before it was distinct from other branches of engineering, several researchers began to explore trial-and-error learning as an engineering principle. The earliest computational investigations of trial-and-error learning were perhaps by Minsky and Farley and Clark, both in 1954. In his Ph.D. dissertation, Minsky discussed computational models of reinforcement learning and described his construction of an analog machine, composed of components he called SNARCs (Stochastic Neural-Analog Reinforcement Calculators). Farley and Clark described another neural-network learning machine designed to learn by trial-and-error. In the 1960s one finds the terms ``reinforcement" and ``reinforcement learning" being widely used in the engineering literature for the first time (e.g., Waltz and Fu, 1965; Mendel, 1966; Fu, 1970; Mendel and McClaren, 1970). Particularly influential was Minsky's paper ``Steps Toward Artificial Intelligence" (Minsky, 1961), which discussed several issues relevant to reinforcment learning, including what he called the credit-assignment problem: how do you distribute credit for success among the many decisions that may have been involved in producing it? All of the methods we discuss in this book are, in a sense, directed toward solving this problem.

The interests of Farley and Clark (1954; Clark and Farley, 1955) shifted from trial-and-error learning to generalization and pattern recognition, that is, from reinforcement learning to supervised learning. This began a pattern of confusion about the relationship between these types of learning. Many researchers seemed to believe that they were studying reinforcement learning when they were actually studying supervised learning. For example, neural-network pioneers such as Rosenblatt (1958) and Widrow and Hoff (1960) were clearly motivated by reinforcement learning---they used the language of rewards and punishments---but the systems they studied were supervised learning systems suitable for pattern recognition and perceptual learning. Even today, reseachers and textbooks often minimize or blur the distinction between these types of learning. Some modern neural-network textbooks use the term trial-and-error to describe networks that learn from training examples because they use error information to update connection weights. This is an understandable confusion, but it substantually misses the essential selectional character of trial-and-error learning.

Partly as a result of these confusions, research into genuine trial-and-error learning became rare in the the 1960s and 1970s. In the next few paragraphs we discuss some of the exceptions and partial exceptions to this trend.

One of these was the work by a New Zealand researcher named John Andreae. Andreae (1963) developed a system called STeLLA that learned by trial and error in interaction with its environment. This system included an internal model of the world and, later, an ``internal monologue" to deal with problems of hidden state (Andreae, 1969a). Andreae's later work placed more emphasis on learning from a teacher, but still included trial-and error (Andreae, 1977). Unfortunately, Andreae's pioneering research was not well-known, and did not greatly impact subsequent reinforcement learning research.

More influential was the work of Donald Michie. In 1961 and 1963 he described a simple trial-and-error learning system for learning how to play Tic-Tac-Toe (or Noughts and Crosses) called MENACE (for Matchbox Educable Noughts and Crosses Engine). It consisted of a matchbox for each possible game position, each containing a number of colored beads, a color for each possible move from that position. By drawing a bead at random from the matchbox corresponding to the current game position, one could determine MENACE's move. When a game was over, beads were added or removed from the boxes used during play to reinforce or punish MENACE's decisions. Michie and Chambers (1968) described another Tic-Tac-Toe reinforcement learner called GLEE (Game Learning Expectimaxing Engine) and a reinforcement learning controller called BOXES. They applied BOXES to the task of learning to balance a pole hinged to a movable cart on the basis of a failure signal occuring only when the pole fell or the cart reached the end of a track. This task was adapted from the earlier work of Widrow and Smith (1964), who used supervised learning methods, assuming instruction from a teacher already able to balance the pole. Michie and Chamber's version of pole-balancing is one of the best early examples of a reinforcement learning task under conditions of incomplete knowledge. It influenced much later work in reinforcement learning, beginning with some of our own studies (Barto, Sutton and Anderson, 1983; Sutton, 1984). Michie has consistently emphasized the role of trial-and-error and learning as essential aspects of artificial intelligence (Michie, 1974).

Widrow, Gupta, and Maitra (1973) modified the LMS algorithm of Widrow and Hoff (1960) to produce a reinforcement learning rule that could learn from success and failure signals instead of from training examples. They called this form of learning ``selective bootstrap adaptation" and described it as ``learning with a critic" instead of ``learning with a teacher." They analyzed this rule and showed how it could learn to play blackjack. This was an isolated foray into reinforcement learning by Widrow, whose contributions to supervised learning were much more influential.

Research on learning automata had a more direct influence on the trial-and-error thread of modern reinforcement learning research. These were methods for solving a non-associative, purely selectional learning problem known as the n -armed bandit by anology to a slot-machine, or ``one-armed bandit," except with n levers (see Chapter 2). Learning automata were simple, low-memory machines for solving this problem. Tsetlin (1973) introduced these machines in the west, and excellent surveys are provided by Narendra and Thatachar (1974, 1989). Barto and Anadan (1985) extended these methods to the associative case.

John Holland (1975) outlined a general theory of adaptive systems based on selectional principles. His early work concerned trial and error primarily in its non-associative form, as in evolutionary methods and the n -armed bandit. In 1986 he introduced classifier systems, true reinforcement-learning systems including association and value functions. A key component of Holland's classifer systems was always a genetic algorithm, an evolutionary method whose role was to evolve useful representations. Classifier systems have been extensively developed by many researchers to form a major branch of reinforcement learning research (e.g., see text by Goldberg, 1989; and Wilson, 1994), but genetic algorithms---which by themselves are not reinforcement learning systems---have received much more attention.

The individual most responsible for reviving the trial-and-error thread to reinforcement learning within artificial intelligence is Harry Klopf (1972, 1975, 1982). Klopf recognized that essential aspects of adaptive behavior were being lost as learning researchers came to focus almost exclusively on supervised learning. What was missing, according to Klopf, were the hedonic aspects of behavior, the drive to achieve some result from the environment, to control the environment toward desired ends and away from undesired ends. This is the essential idea of reinforcement learning. Klopf's ideas were especially influential on the authors because our assessment of them (Barto and Sutton, 1981b) led to our appreciation of the distinction between supervised and reinforcement learning, and to our eventual focus on reinforcement learning. Much of the early work that we and colleagues accomplished was directed toward showing that reinforcement learning and supervised learning were indeed very different (Barto, Sutton, and Brouwer, 1981; Barto and Sutton, 1981a; Barto and Anandan, 1985). Other studies showed how reinforcement learning could address important problems in neural-network learning, in particular, how it could produce learning algorithms for multi-layer networks (Barto, Anderson, and Sutton, 1982; Barto and Anderson, 1985; Barto and Anandan, 1985; Barto, 1985; Barto, 1986; Barto and Jordan, 1986).

We turn now to the third thread to the history of reinforcement learning, that concerning temporal-difference learning. Temporal-difference learning methods are distinctive in being driven by the difference between temporally successive estimates of the same quantity, for example, of the probability of winning in the Tic-Tac-Toe example. This thread is smaller and less distinct than the other two, but has played a particularly important role in the field, in part because temporal-difference methods seem to be new and unique to reinforcement learning.

The origins of temporal-difference learning are in part in animal learning psychology, in particular, in the notion of secondary reinforcers. A secondary reinforcer is a stimulus that has been paired with a primary reinforcer such as food or pain and, as a result, has come to take on similar reinforcing properties. Minsky (1954) may have been the first to realize that this psychological principle could be important for artificial learning systems. Arthur Samuel (1959) was the first to propose and implement a learning method that included temporal-difference ideas, as part of his celebrated checkers-playing program. Samuel made no reference to Minsky's work or to possible connections to animal learning. His inspiration apparently came from Claude Shannon's (1950a) suggestion that a computer could be programmed to use an evaluation function to play chess, and that it might be able to to improve its play by modifying this function online. (It is possible that these ideas of Shannon also influenced Bellman, but we know of no evidence for this.) Minsky (1961) extensively discussed Samuel's work in his ``Steps" paper, suggesting the connection to secondary reinforcement theories, natural and artificial.

As we have discussed, in the decade following the work of Minsky and Samuel, little computational work was done on trial-and-error learning, and apparently no computational work at all was done on temporal-difference learning.

In 1972, Klopf brought trial-and-error learning together with an important component of temporal-difference learning. Klopf was interested in principles that would scale to learning in very large systems, and thus was intrigued by notions of local reinforcement, whereby subcomponents of an overall learning system could reinforce one another. He developed the idea of ``generalized reinforcement," whereby every component (nominally, every neuron) viewed all of its inputs in reinforcement terms, excitatory inputs as rewards and inhibitory inputs as punishments. This is not the same idea as what we now know as temporal-difference learning, and in retrospect it is farther from it than was Samuel's work. Nevertheless, Klopf's work also linked the idea with trial-and-error learning and with the massive empirical database of animal learning psychology.

Sutton (1978a--c) developed Klopf's ideas further, particularly the links to animal learning theories, describing learning rules driven by changes in temporally successive predictions. He and Barto refined these ideas and developed a psychological model of classical conditioning based on temporal-difference learning (Sutton and Barto, 1981; Barto and Sutton, 1982). There followed several other influential psychological models of classical conditioning based on temporal-difference learning (e.g., Klopf, 1988; Moore et al., 1986; Sutton and Barto, 1987, 1990). Some neuroscience models developed at this time are well interpreted in terms of temporal-difference learning (Hawkins and Kandel, 1984; Byrne, 1990; Gelperin et al., 1985; Tesauro, 1986; Friston et al, 1994), although in most cases there was no historical connection. A recent summary of links between temporal-difference learning and neuroscience ideas is provided by Schultz, Dayan, and Montague, 1997).

In our work on temporal-difference learning up until 1981 we were strongly influenced by animal learning theories and by Klopf's work. Relationships to Minsky's ``Steps" paper and to Samuel's checkers players appear to have been recognized only afterwards. By 1981, however, we were fully aware of all the prior work mentioned above as part of the temporal-difference and trial-and-error threads. At this time we developed a method for using temporal-difference learning in trial-and-error learning, known as the actor-critic architecture, and applied this method to Michie and Chambers' pole-balancing problem (Barto, Sutton and Anderson, 1983). This method was extensively studied in Sutton's (1984) PhD thesis and extended to use backpropagation neural networks in Anderson's (1986) PhD thesis. Around this time, Holland (1986) incorporated temporal-difference methods explicitly into his classifier systems. A key step was taken by Sutton in 1988 by separating temporal-difference learning from control, treating it as a general prediction method. That paper also introduced the TD(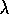) \ algorithm and proved some of its convergence properties.

As we were finalizing our work on the actor-critic architecture in 1981, we discovered a paper by Ian Witten (1977) which contains the earliest known publication of a temporal-difference learning rule. He proposed the method that we now call TD(0) for use as part of an adaptive controller for solving MDPs. Witten's work was a descendant of Andreae's early experiments with STeLLA and other trial-and-error learning systems. Thus, Witten's 1977 paper spanned both major threads of reinforcement-learning research---trial-and-error and optimal control---while making a distinct early contribution to temporal-difference learning.

Finally, the temporal-difference and optimal control threads were fully brought together in 1989 with Chris Watkins's development of Q-learning. This work extended and integrated prior work in all three threads of reinforcement learning research. Paul Werbos (1987) also contributed to this integration by arguing for the convergence of trial-and-error learning and dynamic programming since 1977. By the time of Watkins's work there had been tremendous growth in reinforcement learning research, primarily in the machine learning subfield of artificial intelligence, but also in neural networks and artificial intelligence more broadly. In 1992, the remarkable success of Gerry Tesauro's backgammon playing program, TD-Gammon, brought additional attention to the field. Other important contributions made in the recent history of reinforcement learning are too numerous to mention in this brief account; we cite these at the end of the individual chapters in which they arise.