CMPUT 325: Assignment 7

	Reinforcement Learning and Artificial Intelligence (RLAI)
	CMPUT 325: Assignment 7

Due: Monday, Dec 4, 2006 by 23:59:59

Specs:

Given a database of edges and nodes representing an undirected graph, e.g.

node(a). node(b). node(c). node(d). edge(a,b). edge(b,c). edge(c,a). edge(a,d). edge(c,d).

write the following prolog predicates.

1. connect(+X,+L). Define the predicate connect/2 which tells you if the node X is directly connected to every node in the list L.

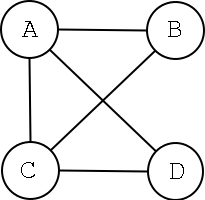?- connect(a,[b,c]).

yes

?- connect(b,[c]).

yes

?- connect(b,[a,c,d]).

no

2. simple_path(+X,+Y,-P). Define the predicate simple_path/3. Given two nodes X and Y, P should contain a path between X and Y in the graph which does not revisit any node. Upon asking the prolog engine for more results, every such path should be produced.

?- simple_path(a,d,X).

X = [a,b,c,d] ? ;

X = [a,c,d] ? ;

X = [a,d] ? ;
no

3. hamiltonian_path(-P). Define the predicate hamiltonian_path/1. P should contain a path between any two nodes in the graph which visits every node exactly once. Upon asking the prolog engine for more results, every such path should be produced.

?- hamiltonian_path(L).

L = [a,d,c,b] ? ;

L = [a,b,c,d] ? ;

L = [b,c,d,a] ? ;

L = [b,a,d,c] ? ;

L = [b,c,a,d] ? ;

L = [b,a,c,d] ? ;

L = [c,d,a,b] ? ;

L = [c,b,a,d] ? ;

L = [d,c,b,a] ? ;

L = [d,a,c,b] ? ;

L = [d,c,a,b] ? ;

L = [d,a,b,c] ? ;

no

4. hamiltonian_cycle(-C). Define the predicate hamiltonian_cycle/1. C should contain a path between any two nodes in the graph which visits every node exactly once and where the first node in the path is connected to the final node in the path. Upon asking the prolog engine for more results, every such path should be produced.

?- hamiltonian_cycle(L).

L = [a,d,c,b] ? ;

L = [a,b,c,d] ? ;

L = [b,c,d,a] ? ;

L = [b,a,d,c] ? ;

L = [c,d,a,b] ? ;

L = [c,b,a,d] ? ;

L = [d,c,b,a] ? ;

L = [d,a,b,c] ? ;

no

5. This question uses the sicstus finite domain constraint problem solver. This will be discussed in class. Notes on its use can be found at http://www.cs.ualberta.ca/~you/courses/325/Mynotes/Log/clp-intro.html.

In order to make use of the FD constraint solver, at the top of your file, add the line:
:- use_module(library(clpfd)).

For this question, we will be scheduling a week's worth of meals at a prix fixe restaurant. The following constraints must be observed:

The restaurant offers two meals on weekdays (Monday through Friday) and three meals on weekends (Saturday and Sunday)
Each meal is centred around a theme of vegetables, meat or fish
Only one meal of each theme may be offered in any night. Also, obviously, each of the two (or three) meals offered in a night must be distinct.
If a meal is offered one night, it cannot be re-offered until at least two days have passed. Remember that Sunday and Monday are adjacent days of the week. A meal offered on Sunday, then, could not be offered on Monday or Tuesday (and, of course, could have been offered on Friday or Saturday)
Certain themes must or must not be offered on certain nights:

A fish-themed meal must be offered on Friday
A meat-themed meal must be offered on Tuesday and Thursday
sushi must be one of the themes offered on Saturday
sushi may not be offered on Tuesday
falafel must be one of the themes offered on Monday

Define the predicate menu/5, which takes parameters of the form menu(-X, +D, +V, +M, +F). D contains a flat list of the themes of the various meals offered. V, M, and F are a count of the number of vegetable-, meat- and fish-themed meals in the list D. D will be ordered such that all vegetable-themed meals come first, followed by meat-themed meals and fish-themed meals. falafel is guaranteed to be the first vegetable-themed meal and sushi is guaranteed to be the first fish-themed meal.

menu should bind X to a list of the form

X =
[[M1,M2],[T1,T2],[W1,W2],[R1,R2],[F1,F2],[S1,S2,S3],[X1,X2,X3]]

, where M1 contains the first of two meals offered on Monday, and M2 the second of the two meals offered on Monday, and so on. Each entry in X will be the index of the meal in the list D (with 1 being falafel). One further constraint is imposed here, in order to reduce the number of possible results. The order of the meals presented for each evening should be the same as in the list D.

For example:

menu(X,[falafel,v2,v3,m1,m2,sushi,f2,f3],3,2,3).

X 
= [[1,7],[2,4],[3,6],[5,8],[1,7],[2,4,6],[3,5,8]] ?

yes

Meaning that Monday is serving falafel and f2 (sounds tasty), Tuesday is serving v2 and m1, and so on.

Due to the large spaces being searched, it may take a while to find all possible menus. Your code should enumerate all possibilities and fail (print no) when no more can be found.

Submission Instructions:

Write all your answers in a plain text file named a7. From the directory where this file is located, type in the following command:

astep -c c325 -p ex7 a7

When prompted if this is your primary submission, answer Y. You may submit as many times as you like; the last version you submit will be marked. All submissions should be primary submissions, not just the last.

Ensure that you follow the Style and Submission Guidelines exactly. Failure to do so will result in lost marks.

Rules, Guidelines and Suggestions:

The notation + in the specs above means that the variable will always be instantiated when the predicate is called. The -, on the other hand, means that the variable will always be uninstantiated.
Ensure that you remove or comment out all definitions of nodes and edges from your submitted file.
You may find it useful for part 1 and beyond to define a rule joined(A,B) which is true if either edge(A,B) or edge(B,A) is in the database.
Do not use the disjunction operator (;) for questions 1 through 4. You may use it for question 5.
Do not use the cut (!) or the not (\+).
Do not use the if-then-else predicate (-> ;).

You may find the following primitive predicates helpful:

   X is E  True if X matches the value of the arithmetic expression E;
           Normally, X is a variable and the result of matching will have   
           X bound to the result of evaluating E. Therefore, E must be 
           an alrithmetic expression. 

   X = Y   True if X and Y are unifiable

   E1 =:= E2  True if the values of arithmetic exps E1 and E2 are equal

   E1 =\= E2  True if the values of arithmetic exps E1 and E2 are not equal

   T1 == T2   True if T1 and T2 are identical

   T1 \== T2  True if T1 and T2 are not identical

You will definitely find the built-in predicate findall/3 helpful.
findall finds all data that matches a certain goal. For example, the goal findall(A,node(A),Nodes) determines all possible A for which the goal node(A) is true. It then places them in the list Nodes. So findall(A,node(A),Nodes)for the graph above would bind Nodes to the list [a,b,c,d].
Try your code with graphs other than the simple graph given above.
Block comments in Prolog code are delimited with /* and */, end of line comments start with the character %.
You must use the finite domain constraint solver for question 5.

Possibly Helpful Predicates

not_member(_,[]).

not_member(X,[Y|Xs]) :- 

  X \== Y, 

  not_member(X,Xs).



member(X,[X|_]).

member(X,[Y|Xs]) :-

    X \== Y,

    member(X,Xs).



append([], L, L).

append([H|T], L, [H|R]) :-

  append(T, L, R).

Some Starting Code for Q5





menu(X,D,V,M,F) :-

    X =
[[M1,M2],[T1,T2],[W1,W2],[R1,R2],[F1,F2],[S1,S2,S3],[X1,X2,X3]],

    Total =
[M1,M2,T1,T2,W1,W2,R1,R2,F1,F2,S1,S2,S3,X1,X2,X3],



    /*calculate upper value of domain*/



    domain(Total,1,/*insert upper value of domain
here*/),



    /*set up constraints here*/



    labeling([],Total).

/* if you want to see the menus you are creating, include the
following goal after labeling.  Make sure this goal is not

part of the menu rule when you submit your assignment */

%print_it(X,D,[mon,tue,wed,thu,fri,sat,sun]).



element_at(X,[X|_],1).

element_at(X,[_|L],K) :- 

    K > 1, 

    K1 is K - 1, 

    element_at(X,L,K1).

print_it([],_,_).

print_it([[X1,X2]|Xs],M,[D|Ds]) :-

    write(D), write(': '),

    element_at(D1,M,X1),

    element_at(D2,M,X2),

    write(D1),write(' '),write(D2),nl,

    print_it(Xs,M,Ds).

print_it([[X1,X2,X3]|Xs],M,[D|Ds]) :-

    write(D), write(': '),

    element_at(D1,M,X1),

    element_at(D2,M,X2),

    element_at(D3,M,X3),

    write(D1),write(' '),write(D2),write('
'),write(D3),nl,

    print_it(Xs,M,Ds).

Mark Breakdown:

Question	Marks
1	2
2	4
3	5
4	3
5	6
Total	20
Cumulative Total	168

Back to CMPUT 325 Homepage

Extend this Page How to edit Style Subscribe Notify Suggest Help This open web page hosted at the University of Alberta. Terms of use 1600/0