


In this book we try to present a uniform approach to a wide class of tasks, but of course there are always exceptional tasks that are better treated in a specialized way. For example, our general approach involves learning an action-value function, but in Chapter 1 we presented a TD method for learning to play Tic-Tac-Toe that learned something much more like a state-value function. If we look closely at that example, it becomes apparent that the function learned there is neither an action-value function nor a state-value function in the usual sense. A conventional state-value function evaluates states in which the agent has the option of selecting an action, but the state-value function used in Tic-Tac-Toe evaluates board positions after the agent has made its move. Let us call these after states, and value functions over these after-state value functions. After states are useful when we have knowledge of an initial part of the environment's dynamics but not necessarily of the full dynamics. For example, in games we typically know the immediate effects of our moves. We know for each possible chess move what the resulting position will be, but not how our opponent will reply. After-state value functions are a natural way to take advantage of this kind of knowledge and thereby produce a more efficient learning method.
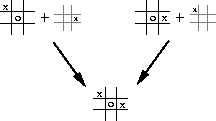
The reason it is more efficient to design algorithms in terms of after states is apparent from the Tic-Tac-Toe example. A conventional action-value function would map from positions and moves to an estimate of the value. But many position-move pairs produce the same resulting position, as in this example:

In such cases the position-move pairs are different, but produce the same ``after position" and thus must have the same value. A conventional action-value function would have to separately assess both pairs, whereas an after-state value function would immediately assess both equally. Any learning about the position-move pair on the left would immediately transfer to the pair on the right.
After states arise in many tasks, not just games. For example, in queuing tasks there are actions such as assigning customers to servers, rejecting customers, or discarding information. In such cases the actions are in fact defined in terms of their immediate effects, which are completely known. For example, in the access-control queuing example described in the previous section, a more efficient learning method could be obtained by breaking the environment's dynamics into the immediate effect of the action, which is deterministic and completely known, and the unknown random processes having to do with the arrival and departure of customers. The after-states would be the number of free servers after the action, but before the random processes had produced the next conventional state. Learning an after-state value function over the after states would enable all actions which produced the same number of free servers to share experience. This should result is a significant reduction in learning time.
It is impossible to describe all the possible kinds of specialized problems and corresponding specialized learning algorithms. However, the principles developed in this book should apply widely. For example, after-state methods are still aptly described in terms of generalized policy iteration, with a policy and (after-state) value function interacting in essentially the same way. In many cases one will still face the choice between on-policy and off-policy methods for managing the need for persistent exploration.
Exercise  .
.
Describe how the task of Jack's Car Rental (Example 4.2) could be reformulated in terms of after states. Why, in terms of this specific task, would such a reformulation be likely to speed convergence?


