- ... selection.2.1
- The difference between instruction and evaluation can be clarified by contrasting two
types of function optimization algorithms. One type is used when information about
the gradient of the function being minimized (or maximized) is directly
available. The gradient instructs the algorithm as to how it should move in the
search space. The errors used by many supervised learning algorithms are gradients (or
approximate gradients). The other type of optimization algorithm uses only function
values, corresponding to evaluative information, and has to actively probe the
function at additional points in the search space in order to decide where to go next.
Classical examples of these types of algorithms are, respectively, the
Robbins-Monro and the Kiefer-Wolfowitz stochastic approximation algorithms (see,
e.g., Kashyap, Blaydon, and Fu, 1970).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... probability.2.2
- Our description is actually a considerable
simplification of these learning automata algorithms. For example, they are
defined as well for
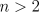 and often use a different step-size parameter on success and on
failure. Nevertheless, the limitations identified in this section still apply.
and often use a different step-size parameter on success and on
failure. Nevertheless, the limitations identified in this section still apply.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... agent.3.1
- We use the terms agent, environment, and action instead of the engineers' terms controller, controlled system (or plant), and control
signal because they are meaningful to a wider audience.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
 .3.2
.3.2
- We restrict attention to
discrete time to keep things as simple as possible, even though many of
the ideas can be extended to the continuous-time case (e.g., see Bertsekas and
Tsitsiklis, 1996; Werbos, 1992; Doya,
1996).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
 .3.3
.3.3
- We
use
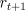 instead of
instead of 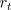 to denote the immediate reward due to the action
taken at time
to denote the immediate reward due to the action
taken at time  because it emphasizes that
the next reward and the next state,
because it emphasizes that
the next reward and the next state,  , are jointly determined.
, are jointly determined.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... do.3.4
- Better places for imparting
this kind of prior knowledge are the initial policy or value function, or in
influences on these. See Lin (1992),
Maclin and Shavlik (1994), and
Clouse (1996).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...episodes,3.5
- Episodes are often called
"trials" in the literature.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
both3.6
- Ways to formulate tasks that are both continuing and
undiscounted are the subject of current research (e.g., Mahadevan,
1996; Schwartz,
1993; Tadepalli and Ok, 1994). Some of the
ideas are discussed in Section 6.7.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
journey.6.1
- If this were a control problem with the objective of minimizing
travel time, then we would of course make the rewards the negative
of the elapsed time. But since we are concerned here only with prediction (policy
evaluation), we can keep things simple by using positive numbers.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... policies.9.1
- There are interesting exceptions to
this. See, e.g., Pearl (1984).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.