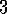 .
.



The reinforcement learning problem is obviously deeply indebted to the idea of Markov decision processes from the field of optimal control. These historical influences and other major influences from psychology are described in the brief history given in Chapter 1. Reinforcement learning adds to MDPs a focus on approximation and incomplete information for realistically large problems. MDPs and the reinforcement learning problem are only weakly linked to traditional learning and decision-making problems in artificial intelligence. However, artificial intelligence is now vigorously exploring MDP formulations for planning and decision making from a variety of perspectives. MDPs are more general than previous formulations used in artificial intelligence problem in that they permit more general kinds of goals and uncertainty.
Our presentation of the reinforcement learning problem was influenced by Watkins (1989).
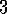 .
.
The bio-reactor example is based on the work of Ungar (1990) and Miller and Williams (1992). The recycling robot example was inspired by the can-collecting robot built by Jonathan Connell (1989).
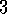 .
. -- 3.4
-- 3.4
The terminology of episodic and continual tasks is different from that usually used in the MDP literature. In that literature it is common to distinguish three types of tasks: 1) finite-horizon tasks, in which interaction terminates after a particular fixed number of time steps; 2) indefinite-horizon tasks, in which interaction can last arbitrarily long but must eventually terminate; and 3) infinite-horizon tasks, in which interaction does not terminate. Our episodic and continual tasks are similar to indefinite-horizon and infinite-horizon tasks, respectively, but we prefer to emphasize the difference in the nature of the interaction. This difference seems more fundamental than the difference in the objective functions emphasized by the usual terms. Often episodic tasks use an indefinite-horizon objective function and continual tasks an infinite-horizon objective function, but we see this as a common coincidence rather than a fundamental difference.
The pole-balancing example is from Barto, Sutton, and Anderson (1983) and Michie and Chambers (1968).
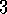 .
.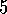
For an excellent discussion of the concept of state see Minsky (1967).
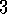 .
.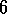
The theory of Markov decision processes (MDPs) is treated by, e.g., Bertsekas (1995), Ross (1983), White (1969), and Whittle (1982, 1983). This theory is also studied under the heading of stochastic optimal control, where adaptive optimal control methods are most closely related to reinforcement learning (e.g., Kumar, 1985; Kumar and Varaiya, 1986).
The theory of MDPs evolved from efforts to understand the problem of making sequences of decisions under uncertainty, where each decision can depend on the previous decisions and their outcomes. It is sometimes called the theory of multi-stage decision processes, or sequential decision processes, and has roots in the statistical literature on sequential sampling beginning with the papers by Thompson (1933, 1934) and Robbins (1952) that we cited in Chapter 2 in connection with bandit problems (which are prototypical MDPs if formulated as multiple-situation problems).
The earliest instance of which we are aware in which reinforcement learning was discussed using the MDP formalism is Andreae's (1969b) description of a unified view of learning machines. Witten and Corbin (1973) experimented with a reinforcement learning system later analyzed by Witten (1977) using the MDP formalism. Although he did not explicitly mention MDPs, Werbos (1977) suggested approximate solution methods for stochastic optimal control problems that are related to modern reinforcement learning methods (see also Werbos, 1982, 1987, 1988, 1989,1992). Although Werbos' ideas were not widely recognized at the time, they were prescient in emphasizing the importance of approximately solving optimal control problems in a variety of domains, including artificial intelligence. The most influential integration of reinforcement learning and MDPs is due to Watkins (1989). His treatment of reinforcement learning using the MDP formalism has been widely adopted.
Our characterization of the reward dynamics of an MDP in terms of
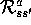 is slightly unusual. It is more common in the MDP literature to
describe the reward dynamics in terms of the expected next reward given just
the current state and action, i.e., by
is slightly unusual. It is more common in the MDP literature to
describe the reward dynamics in terms of the expected next reward given just
the current state and action, i.e., by
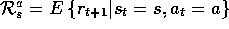 . This quantity is related to our
. This quantity is related to our 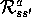 as
follows:
as
follows:
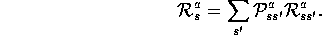
In conventional MDP theory, 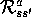 always appears in an expected value sum
like this one, and therefore it is easier to use
always appears in an expected value sum
like this one, and therefore it is easier to use 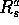 . In reinforcement
learning, however, we more often have to refer to individual actual or sample
outcomes. For example, in the recycling robot, the expected reward for the
action search in state low depends on the next state
(Table 3.1). In teaching reinforcement learning, we have
found the
. In reinforcement
learning, however, we more often have to refer to individual actual or sample
outcomes. For example, in the recycling robot, the expected reward for the
action search in state low depends on the next state
(Table 3.1). In teaching reinforcement learning, we have
found the 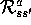 notation to be more straightforward conceptually and easier
to understand.
notation to be more straightforward conceptually and easier
to understand.
 .
. and 3.8
and 3.8
Assigning value based on what is good or bad in the long run has ancient roots.
In control theory, mapping states to numerical values representing the long-term consequences of control decisions is a key part of optimal control theory, which was developed in the 1950s by extending 19th century state-function theories of classical mechanics (see, for example, Schultz and Melsa, 1967). In describing how a computer could be programmed to play chess, Shannon (1950b) suggested using an evaluation function that took into account the long-term advantages and disadvantages of a chess position.
Watkins's (1989) Q-learning algorithm for estimating 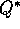 (Chapter 6
) made
action-value functions an important part of reinforcement learning, and
consequently these functions are often called Q-functions. But the idea of an
action-value function is much older than this. Shannon
(1950b) suggested that a function
(Chapter 6
) made
action-value functions an important part of reinforcement learning, and
consequently these functions are often called Q-functions. But the idea of an
action-value function is much older than this. Shannon
(1950b) suggested that a function 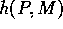 could be used
by a chess-playing program to decide whether a move M in position P is
worth exploring. Michie's (1961, 1963) MENACE
system and Michie and Chambers (1968) BOXES system
can be understood as estimating action-value functions. In classical physics,
Hamilton's principle function is an action-value function: Newtonian dynamics
are greedy with respect to this function (e.g., Goldstein,
1957). Action-value functions also played a central in
Denardo's (1967) theoretical treatment of DP in terms of
contraction mappings.
could be used
by a chess-playing program to decide whether a move M in position P is
worth exploring. Michie's (1961, 1963) MENACE
system and Michie and Chambers (1968) BOXES system
can be understood as estimating action-value functions. In classical physics,
Hamilton's principle function is an action-value function: Newtonian dynamics
are greedy with respect to this function (e.g., Goldstein,
1957). Action-value functions also played a central in
Denardo's (1967) theoretical treatment of DP in terms of
contraction mappings.
What we call the Bellman equation for 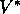 was first introduced by Richard
Bellman (1957) who called it the ``basic functional equation." The
counterpart of the Bellman optimality equation for continuous time and state
problems is known as the Hamilton-Jacobi-Bellman equation (or often just the
Hamilton-Jacobi equation), indicating its roots in classical physics (e.g., Schultz
and Melsa, 1967).
was first introduced by Richard
Bellman (1957) who called it the ``basic functional equation." The
counterpart of the Bellman optimality equation for continuous time and state
problems is known as the Hamilton-Jacobi-Bellman equation (or often just the
Hamilton-Jacobi equation), indicating its roots in classical physics (e.g., Schultz
and Melsa, 1967).


